Предположим, что функции и дифференцируемы вместе со своими производными до n-го порядка включительно. Применяя правило дифференцирования произведения двух функций, получим

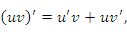
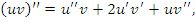
Сопоставим эти выражения со степенями бинома :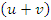

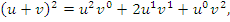
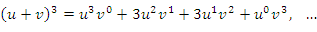
Бросается в глаза правило соответствия: чтобы получить формулу для производной 1-го, 2-го или 3-го порядков от произведения функций и , нужно заменить степен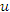и и 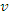в выражении для 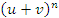(где n = 1,2,3) производными соответствующих порядков. Кроме того, нулевые степени величин 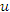и 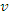следует заменить производными нулевого порядка, подразумевая под ними функции и :

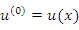
Обобщая это правило на случай производной произвольного порядка n, получим формулу Лейбница,

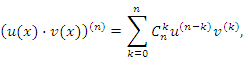
где 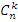- биномиальные коэффициенты:

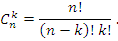
Строгое доказательство формулы Лейбница основывается на методе математической индукции.

Примеры:

Найти производную 10-го порядка от произведения функций и .
Решение. Учитывая, что

получим

Найти производную 15-го порядка от функции .
Решение. Представим функцию в виде произведения двух функций:
Далее,

Таким образом,

Вычислить значение производной n-го порядка от в точке x = 0.
Решение. Продифференцируем и представим результат в виде произведения двух функций,
где i – мнимая единица.
Очевидно, что

Используя формулу Лейбница, получим

Заметим, что
Таким образом,

Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21

Вход на сайт

Поиск

Календарь

Архив записей

2020 Ноябрь

Друзья сайта

Сайт преподавателя математики и информатики Иванской Светланы Алексеевны

Ставропольский край, г. Минеральные Воды