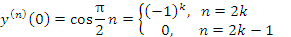Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21

Производные высших порядков
Пусть  – некоторая дифференцируемая функция, производная от которой
– некоторая дифференцируемая функция, производная от которой  также является дифференцируемой функцией. Производная функции
также является дифференцируемой функцией. Производная функции  обозначается символическим выражением
обозначается символическим выражением  и называется второй производной (или производной второго порядка) функции
и называется второй производной (или производной второго порядка) функции  :
:

Запись вида

позволяет указать в явной форме переменную, по которой выполняется дифференцирование функции. Однако такое обозначение является достаточно громоздким и поэтому обычно используется его сокращенная форма:

Эта формула читается как “игрек два штриха равен дэ два игрек по дэ икс дважды”.
Производной n-го порядка от функции  называется производная от производной (n - 1)-го порядка:
называется производная от производной (n - 1)-го порядка:

Верхний индекс n, заключенный в круглые скобки, указывает порядок производной. Например, пятую производную от функции y записывают в виде  . Для обозначения производных до третьего порядка включительно обычно предпочитают использовать штрихи:
. Для обозначения производных до третьего порядка включительно обычно предпочитают использовать штрихи:  или
или  . Если порядок производной
. Если порядок производной  , то для его обозначения допускается использование римских цифр, например,
, то для его обозначения допускается использование римских цифр, например,

Отметим также, что под производной нулевого порядка от функции  понимается сама функция
понимается сама функция  :
:
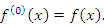
Другими словами, нулевое число преобразований функции означает ее неизменность. Более весомые причины такого соглашения обсуждаются в разделе “Формула Лейбница”.
Если функция задана уравнениями в параметрической форме,

то для вычисления ее производных высших порядков используется цепочка формул



и так далее. Пусть, например,

Тогда


Для нахождения производной n-го порядка неявно заданной функции требуется последовательное вычисление всех ее производных более низкого порядка. Для примера рассмотрим уравнение

определяющее неявно заданную функцию y(x).
Дважды дифференцируя это равенство, получим систему двух уравнений

Если из первого уравнения выразить производную y' и подставить полученный результат во второе уравнение, то останется лишь разрешить преобразованное второе уравнение относительно y''.
Примеры:
|
|
|
|
|
|
|
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21

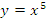 . Тогда
. Тогда






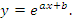




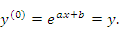





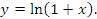




 и, следовательно,
и, следовательно,
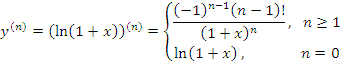






 и вычислить эту производную в точке x = 0. Решение.
и вычислить эту производную в точке x = 0. Решение.




 и, следовательно,
и, следовательно,

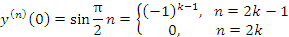
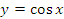 :
: