Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Теорема о непрерывности дифференцируемой функции
Теорема. Если функция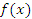 
дифференцируема в некоторой точке a, то она непрерывна в этой точке.
Доказательство. По определению производной
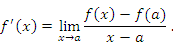
Это предельное равенство означает, что выражение под знаком предела можно представить в виде
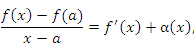
где α(x) – бесконечно малая функция при x → a. Тогда
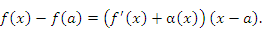
Следовательно,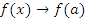 
при x → a.
Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке.
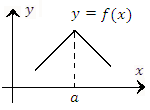
Рис. 8. Непрерывная в точке a функция 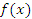не является дифференцируемой в этой точке.
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21