Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Дифференцирование сложной функции
Теорема. Если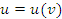 
и 
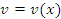– дифференцируемые функции, то производная сложной функции 
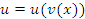равна
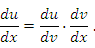
Действительно, производная функции представляет собой отношение дифференциала функции к дифференциалу аргумента. Если сократить общий множитель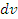 
в числителе и знаменателе выражения в правой части этого равенства, то получим тождество.
Формальное доказательство. По определению производной
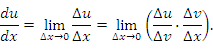
Согласно теореме о непрерывности дифференцируемых функциях,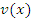 
является непрерывной функцией и, следовательно, 
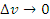при ∆x → 0. Тогда
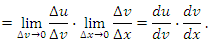
Примеры:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21