Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Логарифмическое дифференцирование
Рассмотрим проблему дифференцирования функций вида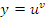 
, где 
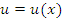и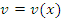 
– некоторые дифференцируемые функции. Используя логарифмические тождества
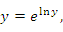
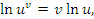
получим
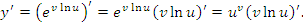
Таким образом, проблема нахождения производных от функций вида 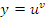сводится к процедуре дифференцирования произведения функций. К такому же результату приводит логарифмическое дифференцирование функции 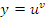, под которым понимается предварительное логарифмирование функции и последующее дифференцирование полученного выражения:
 |
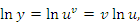
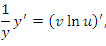
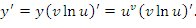(1) |
Правило дифференцирования (1) представляет собой композицию правил дифференцирования показательной и степенной функций. Действительно, запишем формулу (1) в виде
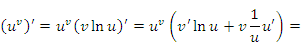
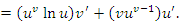
Первый член в правой части этого равенства представляет собой производную от показательной функции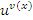 
, где основание u формально рассматривается как константа. Второе слагаемое можно интерпретировать как результат дифференцирования степенной функции 
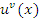, если формально считать, что 
.
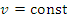Логарифмическое дифференцирование существенно упрощает процедуру вычисления производных от выражений вида
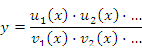
Действительно,
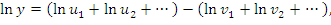
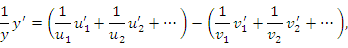
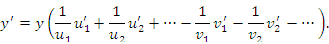
Примеры:
|
. Тогда
|
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21