Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21

Свойства дифференциалов
Пусть 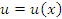 и
и 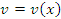 – дифференцируемые функции; c – постоянный множитель. Тогда
– дифференцируемые функции; c – постоянный множитель. Тогда
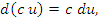

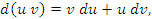
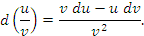
Доказательство. Чтобы проверить справедливость этих равенств, достаточно разделить их правые и левые части на dx. Тогда мы получим стандартные формулы дифференцирования суммы, произведения и частного от деления функций:
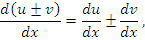
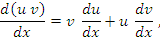
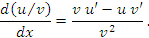
Формальные преобразования, в основе которых лежит определение дифференциала функции, приводят к тем же самым результатам:
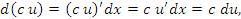
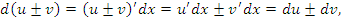
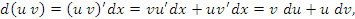
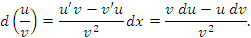
Примеры:
1. 
2. 
3. 
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
