Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Производные степенной, показательной и логарифмической функций
Пусть n – произвольное вещественное число. Тогда
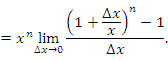
Используя соотношение эквивалентности
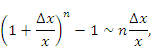
получим, что
Пусть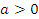 
и 
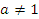. Тогда
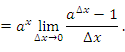
Используя соотношение эквивалентности
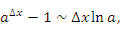
получим правило дифференцирования показательной функции:
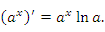
Эта формула принимает особенно простой вид, если основанием является число e:
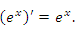
Функция 
является уникальной, ибо это единственная функция, производная от которой совпадает с самой функцией.
Покажем, что для любого x > 0 выполняется следующее правило дифференцирования логарифмической функции:
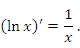
Действительно, приращение этой функции можно представить в виде
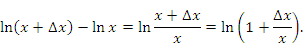
Если ∆x → 0, то бесконечно малая в правой части этого равенства удовлетворяет соотношению эквивалентности
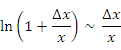
и, следовательно,
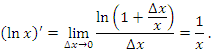
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21