Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Дифференцирование обратной функции
Теорема. Пусть функция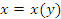 
является обратной для функции 
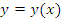. Если существует отличная от нуля производная функции 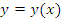по переменной x, то существует и производная обратной функции 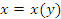по переменной y. При этом
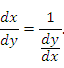
Доказательство. По определению производной
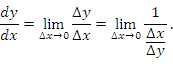
Согласно теореме о непрерывности дифференцируемых функциях,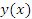 
является непрерывной функцией и, следовательно, 
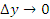при ∆x → 0. Тогда
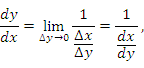
что влечет за собой доказываемое утверждение.
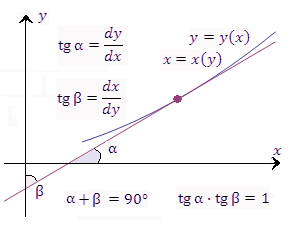
Рис. 9. Геометрическая интерпретация теоремы о дифференцировании обратной функции.
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21