Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Гиперболические функции и их свойства
Гиперболический синус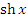 
и гиперболический косинус 
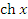определяются аналитическими выражениями
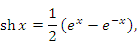
Эти функции определены и непрерывны на всей числовой оси и тождественно удовлетворяют следующим соотношениям, которые легко проверяются непосредственным вычислением:
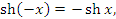
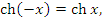
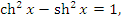
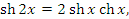
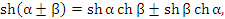
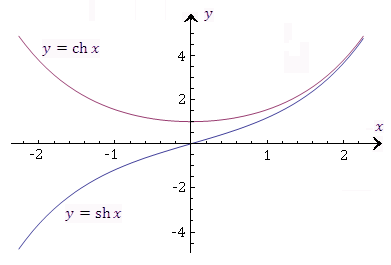
Рис. 3. Графики гиперболических функций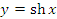 
и 
. График гиперболического косинуса называется цепной линией, которая является линией провисания тяжёлой нити, подвешенной в двух точках.
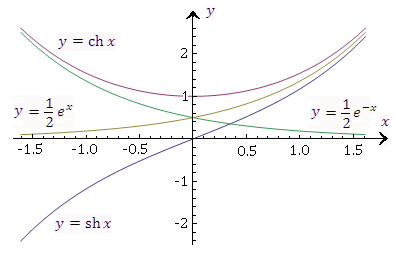
Рис. 4. Сопоставление графиков гиперболических и экспоненциальных функций.
Гиперболический тангенс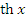 
и гиперболический котангенс 
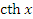определяются формулами
и представляют собой нечетные функции:
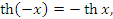
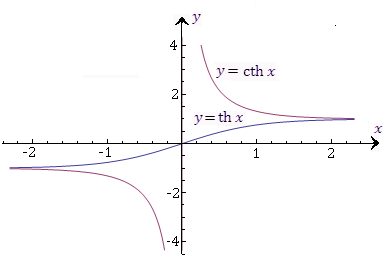
Рис. 5. Графики гиперболических функци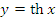й 
и 
.
Рис. 6. Сопоставление графиков функций 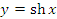, 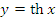и y = x.
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21