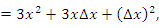Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21

Средняя и мгновенная скорости изменения функции
Существуют различные характеристики, позволяющие детально описывать поведение функции в окрестности заданной точки. Одной из таких характеристик является средняя скорость изменения функции 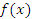 на промежутке
на промежутке 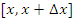 , которая представляет собой отношение изменения функции
, которая представляет собой отношение изменения функции 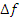 к соответствующему изменению аргумента
к соответствующему изменению аргумента 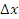 :
:
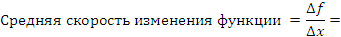 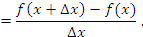 |
(1) |
Термины "изменение аргумента" и "изменение функции" порождают ассоциацию с неким динамическим процессом, в котором аргумент играет роль времени, а функция этого аргумента характеризует пройденный путь или скорость движения частицы. Перечень подобных толкований можно продолжить, подразумевая под изменением функции, например, изменение масса тела, заключенной в сфере малого радиуса, при смещении центра сферы из одной точки в другую и так далее. Поэтому математики отдают предпочтение нейтральным терминам, называя разность 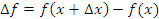 приращением функции, а величину ∆x – приращением аргумента.
приращением функции, а величину ∆x – приращением аргумента.
Пусть, например, 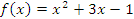 . Тогда средняя скорость изменения функции
. Тогда средняя скорость изменения функции 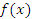 на промежутке [1, 3] равна
на промежутке [1, 3] равна
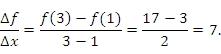
Физическая интерпретация средней скорости изменения функции вполне очевидна. Если 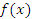 описывает зависимость пройденного частицей пути от времени x ее движения, то
описывает зависимость пройденного частицей пути от времени x ее движения, то 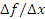 представляет собой среднюю скорость движения частицы за промежуток времени ∆x.
представляет собой среднюю скорость движения частицы за промежуток времени ∆x.
Мгновенная скорость изменения функции представляет собой среднюю скорость изменения функции на бесконечно малом промежутке ∆x. Чем меньше ∆x, тем ближе средняя скорость к мгновенной скорости. Термин “мгновенная скорость изменения функции” выражает суть обсуждаемого понятия, однако обычно мгновенную скорость называют производной функции 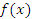 и обозначают символическим выражением
и обозначают символическим выражением 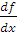 .
.
Таким образом, производная функции 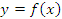 представляет собой предел отношения приращения функции
представляет собой предел отношения приращения функции 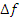 к приращению аргумента
к приращению аргумента 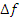 при стремлении последнего к нулю:
при стремлении последнего к нулю:
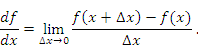 |
(2) |
(Выражение в левой части этого равенства читается как “дэ эф по дэ икс”.) Производная функции 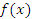 обозначается также символом
обозначается также символом 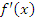 , который читается как “эф штрих от икс”.
, который читается как “эф штрих от икс”.
Функция, имеющая конечную производную в некоторой точке, называется дифференцируемой в этой точке. Говорят, что функция дифференцируема на промежутке, если она дифференцируема в каждой точке этого промежутка.
Производную функции можно найти численно, графически или вычислить с помощью алгебраических формул. Для численного нахождения 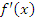 в точке x используется приближенная формула
в точке x используется приближенная формула
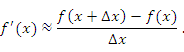 |
(3) |
Проиллюстрируем диапазон применимости этой формулы численными расчетами. Пусть, например, 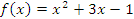 . Результаты вычислений производной функции
. Результаты вычислений производной функции 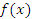 в точке x = 1 при различных значениях ∆x представлены в таблице 1.
в точке x = 1 при различных значениях ∆x представлены в таблице 1.
Таблица 1.
| ∆x | 1 | 0.1 | 0.01 | 0/001 | 0.000001 |
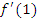 |
6 | 5.1 | 5.01 | 5.001 | 5.000001 |
Очевидно, что последовательность значений 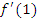 приближается к числу 5 по мере уменьшения ∆x. Поэтому можно предположить, что точное значение
приближается к числу 5 по мере уменьшения ∆x. Поэтому можно предположить, что точное значение 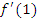 равно пяти. Именно таким и является точное значение.
равно пяти. Именно таким и является точное значение.
Для оценки 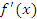 “на лету” достаточно выбрать одно малое значение ∆x и вычислить разностное отношение (3). Более точную оценку дает сбалансированное отношение
“на лету” достаточно выбрать одно малое значение ∆x и вычислить разностное отношение (3). Более точную оценку дает сбалансированное отношение
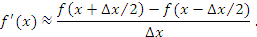 |
(4) |
Примеры:
|
|
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21

 на промежутке [x, x + ∆x]:
на промежутке [x, x + ∆x]:


 на промежутке [x, x + ∆x] равны соответственно
на промежутке [x, x + ∆x] равны соответственно