Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Геометрическая интерпретация производной функции
Обратимся к рисунку 1, на котором представлен фрагмент графика функции 
.
Рис. 1. Секущая AB образует угол β с положительным направлением оси 0x. Касательная к графику функции проведена в точке A.
Угловой коэффициент секущей AB равен средней скорости изменения функции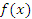 
на промежутке [x, x + ∆x]:
 |
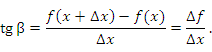(5) |
Предельным положением секущей AB при перемещении точки B к точке A по дуге кривой является касательная к графику в точке A. Поэтому угловой коэффициент касательной равен пределу углового коэффициента секущей при ∆x → 0:
 |
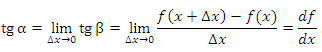(6) |
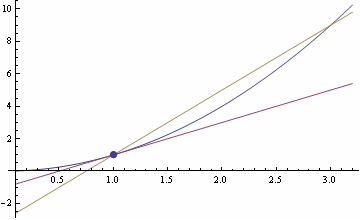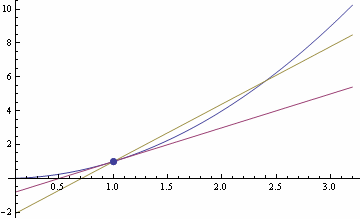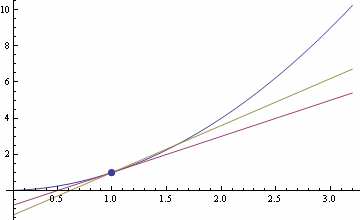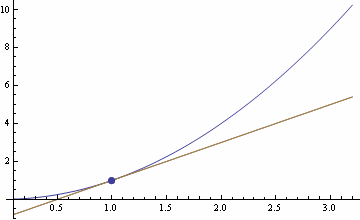
Рис. 2. Касательная является предельным положением секущей AB при перемещении точки B к точке A.
Таким образом, производная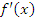 
в точке x равна тангенсу угла, образованного касательной к графику функции в этой точке с положительным направлением оси 0x.
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21