Раздел 9. Начала математического анализа
Тема 9.2 Дифференцирование функций
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21
Дифференциал функции
Под дифференциалом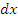 
независимого аргумента понимается приращение аргумента: 
. Совсем иначе определяется дифференциал функции. Согласно определению предела, равенство
означает, что выражение под знаком предела можно представить в виде
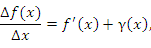
где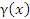 
– бесконечно малая функция более высокого порядка по сравнению с ∆x (при ∆x→0). Тогда приращение функции 
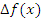описывается формулой
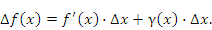
Слагаемое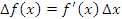 
представляет собой линейную (главную) часть приращения функции и называется дифференциалом функции, который обозначается символом 
:
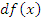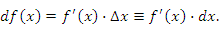
Следовательно, производную функции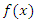 
можно представить в виде отношения дифференциалов 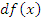и :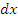
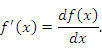
До сих пор запись такого вида рассматривалась нами как единый символ, обозначающий производную функции 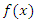. Теперь же это выражение можно интерпретировать как отношение двух дифференциалов: дифференциала функции к дифференциалу аргумента.
Примеры:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21