Раздел 9. Начала математического анализа
Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции
Предел функции
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13
Различные формы неопределенностей
Бесконечно малые величины имеют фундаментальное значение в математическом анализе. Например, понятие предела функции можно сформулировать, положив в основу концепцию бесконечно малой функции. Бесконечно большая функция представляет собой величину, обратную бесконечно малой. Фактически любой раздел дифференциального и интегрального исчисления опирается на анализ бесконечно малых.
Концепция эквивалентных бесконечно малых функций позволяет существенно упростить процедуру раскрытия неопределенностей различного вида и свести вычисление пределов сложных выражений к тривиальным преобразованиям комбинаций степенных функций.
Перечислим основные формы неопределенностей:
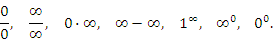
Под неопределенностью вида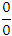 
понимается отношение двух бесконечно малых величин. Неопределенность вида 
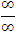возникает при делении одной бесконечно большой величины на другую. Аналогично интерпретируются и другие формы неопределенностей.
Любая форма неопределенности может быть преобразована к неопределенности вида 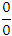. Действительно, пусть 
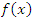и 
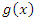– бесконечно большие функции в окрестности некоторой точки. Тогда
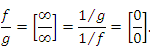
Аналогично,
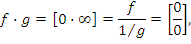
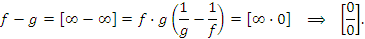
Для преобразования форм неопределенностей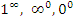 
к виду 
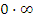(и, следовательно, к виду 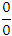) можно использовать логарифмическое тождество
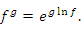
Пусть, например,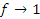 
и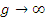 
при x → a. Тогда
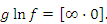
Аналогично,
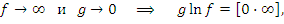
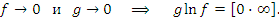
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13