Раздел 9. Начала математического анализа
Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции
Предел функции
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13

Первый замечательный предел
Теорема 1:
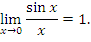
Другая формулировка теоремы 1:
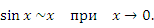
Доказательство. Заметим, что отношение 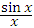 представляет собой четную функцию. Поэтому при анализе поведения этой функции можно ограничиться областью малых положительных значений аргумента x.
представляет собой четную функцию. Поэтому при анализе поведения этой функции можно ограничиться областью малых положительных значений аргумента x.
Пусть x – центральный угол окружности единичного радиуса, выраженный в радианах. Сравним между собой площади фигур, показанных на рисунке 1.
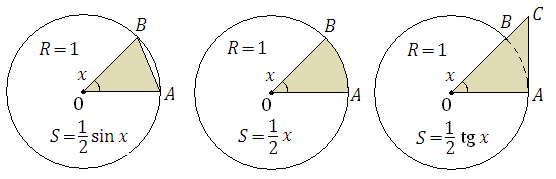
Рис.1. Равнобедренный треугольник AOB, круговой сектор AOB и прямоугольный треугольник AOC.
Очевидно, что для всех 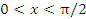 выполняется неравенство
выполняется неравенство
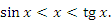
Представим tg x в виде отношения sin x к cos x и разделим обе части этого двойного неравенства на sin x. Тогда неравенство
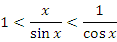
влечет за собой
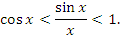
Поскольку 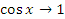 при x → 0, то и
при x → 0, то и 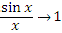 .
.
Графические иллюстрации теоремы 1 представлены на рисунках 2 и 3.
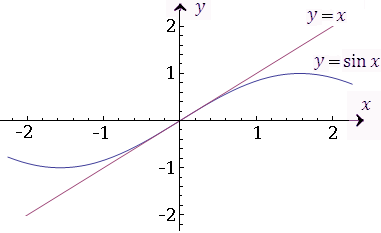
Рис. 2. Прямая y = x является касательной к графику функции 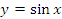 в точке x = 0. Поэтому sin x ≈ x в окрестности нуля.
в точке x = 0. Поэтому sin x ≈ x в окрестности нуля.
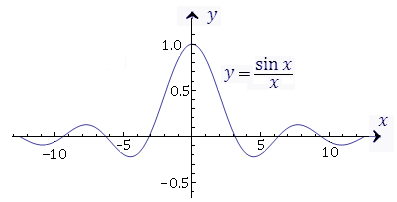
Рис. 3. График функции 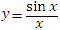 .
.
Теорема 1 допускает следующее очевидное обобщение: если 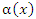 – бесконечно малая величина при x → a, то
– бесконечно малая величина при x → a, то
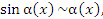

В частности,
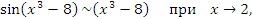
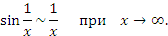
Примеры:
|
|
|
|
|
|
|
|
|
|
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13

 и
и  при x → 0, получим
при x → 0, получим





 влечет за собой
влечет за собой  и
и  при x → 0. Тогда
при x → 0. Тогда



 и
и  при x → 0 воспользуемся тригонометрическим тождеством
при x → 0 воспользуемся тригонометрическим тождеством

 эквивалентной величиной
эквивалентной величиной  :
:








 и
и  , то
, то







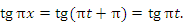
 и, следовательно,
и, следовательно,
