Раздел 9. Начала математического анализа
Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции
Предел функции
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13

Второй замечательный предел
Теорема 2:
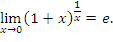
Выбирая 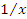 за новую переменную, получим другую форму теоремы 2:
за новую переменную, получим другую форму теоремы 2:
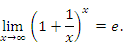
Отметим, что при x → 0 функция 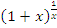 представляет собой неопределенное выражение вида
представляет собой неопределенное выражение вида 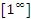 . При этом показателем степени является обратная величина бесконечно малой добавки к единице в основании степени.
. При этом показателем степени является обратная величина бесконечно малой добавки к единице в основании степени.
Если 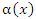 – бесконечно малая функция при x → a, то
– бесконечно малая функция при x → a, то
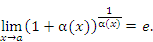
В частности,
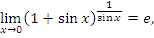
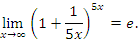
Обсудим процедуру вычисления пределов вида
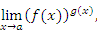
где 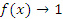 и
и 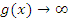 при x → a.
при x → a.
- Сначала представим функцию
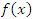 в виде суммы единицы и бесконечно малой величины
в виде суммы единицы и бесконечно малой величины 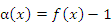 :
:
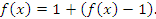
- Затем преобразуем показатель степени
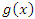 :
:
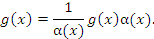
- Учитывая, что
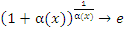 при x → a, получим следующий результат:
при x → a, получим следующий результат:
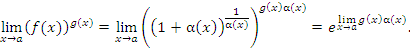
Таким образом, проблема раскрытия неопределенности вида 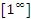 сводится к более простой проблеме раскрытия неопределенности вида
сводится к более простой проблеме раскрытия неопределенности вида 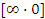 .
.
Проиллюстрируем вышеизложенное простейшим примером:
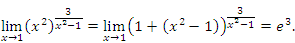
Еще один способ вычисления пределов вида
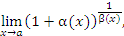
где 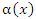 и
и 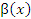 – бесконечно малые функции при x → a, основывается на использовании тождества
– бесконечно малые функции при x → a, основывается на использовании тождества
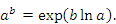
При этом
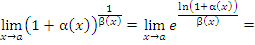
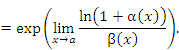
Примеры:
|
|
|
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13




 представляет собой неопределенное выражение вида
представляет собой неопределенное выражение вида  при x → ∞ и, следовательно,
при x → ∞ и, следовательно,






