Бесконечно малые функции

Раздел 9. Начала математического анализа

Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции

Предел функции

Бесконечно малые функции

Свойства бесконечно малых функций

Предел функции

Свойства пределов функций

Сравнение бесконечно малых

Сравнение бесконечно больших

Первый замечательный предел

Второй замечательный предел

Другие важные пределы: Теорема 3

Другие важные пределы: Теорема 4

Другие важные пределы: Теорема 5

Различные формы неопределенностей

Таблица эквивалентных бесконечно малых

Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13

Бесконечно малые функции

 Функция 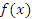   называется бесконечно малой при  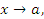, если ее значения по абсолютной величине становятся и остаются меньше любого наперед заданного положительного числа  ε. 

      Приведенное определение полезно для формирования начального представления. В строгой математической формулировке все утверждения должны быть выражены в виде конкретных количественных соотношений. Например, фраза "значения функции становятся и остаются по абсолютной величине меньше любого наперед заданного числа" на математическом языке означает: 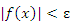   вне зависимости от того, насколько малым выбрано число  ε > 0. Задавая  ε, мы определяем допустимое отклонение функции от нуля. Другими словами, мы готовы считать функцию как бы равной нулю, если ее значения по абсолютной величине не превосходят  ε. 

      Граничные значения  –ε  и  ε  определяют соответствующий интервал 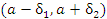 значений независимой переменной  x  в окрестности предельной точки  a. Если перейти к симметричной  δ-окрестности точки  a, определяемой условием

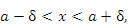(1)

где 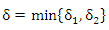 , то неравенство  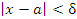  влечет за собой неравенство

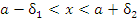(2)

и, следовательно, неравенство

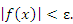(3)

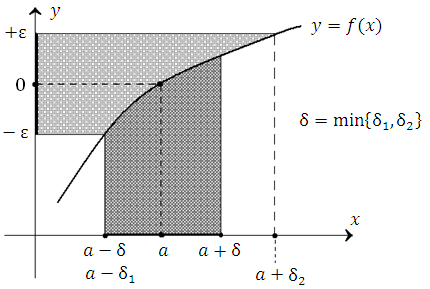
Рис. 1. Для всех значений переменной  x  в интервале 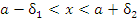   соответствующие значения функции  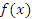  отличаются от нуля не более чем на  ε.

      Таким образом, функция 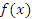   называется бесконечно малой при  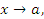, если для любого произвольно малого числа  ε > 0  существует такое число  δ(ε), что для всех  x, удовлетворяющих условию (1), выполняется неравенство (3). Это утверждение записывается с помощью выражения

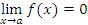
или в виде

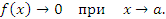
Примеры бесконечно малых функций:     при         при         при         при         при         при         при         при

Пример. Доказать на языке  ε - δ, что Решение. Пусть  ε  – сколь угодно малое положительное число. Найдем множество значений переменной  x, для которых выполняется неравенство . Очевидно, что Полагая  , получим, что условие    влечет за собой неравенство. Тем самым требуемое утверждение доказано.

Пример. Доказать на языке  ε - δ, что Решение. Нужно показать, что для любого сколь угодно малого числа  ε > 0  существует такое число  δ > 0, что для всех  x  из  δ-окрестность точки  x = 1, выполняется неравенство . Действительно, Обозначим   Учитывая, что   выберем Тогда для всех x, удовлетворяющих неравенству выполняется неравенство В частности, Рис. 2. Для любого сколь угодно малого числа  ε > 0  выполняется неравенство    для всех  x  из  δ-окрестности точки  x = 1. Следовательно,

Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13