Раздел 9. Начала математического анализа

Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции

Предел функции

Бесконечно малые функции

Свойства бесконечно малых функций

Предел функции

Свойства пределов функций

Сравнение бесконечно малых

Сравнение бесконечно больших

Первый замечательный предел

Второй замечательный предел

Другие важные пределы: Теорема 3

Другие важные пределы: Теорема 4

Другие важные пределы: Теорема 5

Различные формы неопределенностей

Таблица эквивалентных бесконечно малых

Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13

Другие важные пределы: Теорема 3

Теорема 3:

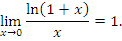
Эквивалентная формулировка теоремы 3:

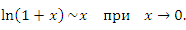
Доказательство. Преобразуем выражение под знаком предела, учитывая свойство логарифмов:

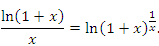
Если  x → 0, то

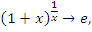
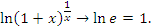
      На рисунке 4 представлена графическая иллюстрация теоремы 3.

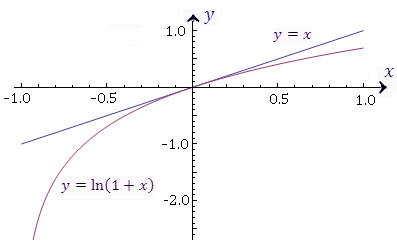
Рис 4. Прямая  y = x  является касательной к графику функции 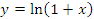   в точке  x = 0  и, следовательно,  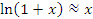  в окрестности нуля.

      Если 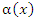   – бесконечно малая функция при  x → a, то

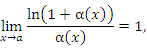
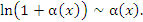
В частности,

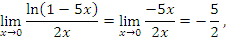
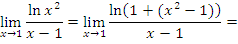
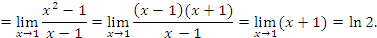
Примеры:

Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13