Раздел 9. Начала математического анализа
Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции
Предел функции
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13
Свойства бесконечно малых функций
Свойство 1. Произведение бесконечно малой функции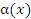 
при 
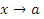и функции 
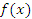, ограниченной в некоторой 
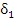-окрестности точки a, есть функция бесконечно малая.
Доказательство. Функция 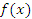является ограниченной в некоторой окрестности точки a и, следовательно, существует такое число B > 0, что
 |
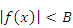(4) |
для всех x, удовлетворяющих условию
 |
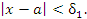(5) |
Поскольку функция 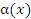является бесконечно малой при 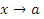, то для любого произвольно малого числа ε > 0 существует такое число 
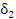, что неравенство
 |
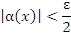(6) |
выполняется для всех x, удовлетворяющих условию
| (7) |
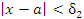
Выберем из чисел 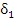и 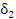наименьшее и обозначим его символом δ. Тогда условие
 |
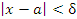(8) |
является более сильным, чем условия (5) и (7) и поэтому влечет неравенства (4) и (6).
Таким образом, для любого произвольно малого числа ε > 0 выполняется неравенство
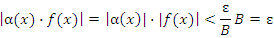
для всех x из δ-окрестности точки a.
Свойство 2. Сумма двух бесконечно малых функций есть функция бесконечно малая.
Доказательство. Пусть ε > 0 – произвольно малое число; 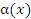и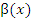 
– бесконечно малые функции при 
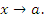. Тогда существуют такие положительные числа 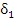и 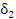, что условия
 |
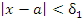(9) |
и
|
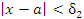(10) |
влекут за собой соответствующие неравенства
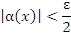
и
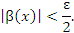
Если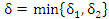 
, то условие 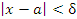перекрывает оба условия (9) и (10) и, следовательно,
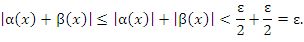
Следствие. Сумма любого конечного числа бесконечно малых функций есть функция бесконечно малая.
Действительно, объединяя элементы такой суммы в группы по два слагаемых и заменяя сумму двух бесконечно малых одной бесконечно малой, получим сумму меньшего числа членов. В конечном итоге сумма любого конечного числа бесконечно малых будет сведена к одной бесконечно малой.
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13