Раздел 9. Начала математического анализа
Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции
Предел функции
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13
Предел функции
Число A называется пределом функции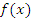 
при 
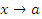, если для любого произвольно малого числа ε > 0 существует такое число δ(ε), что для всех x, удовлетворяющих условию
 |
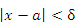(11) |
выполняется неравенство
 |
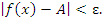(12) |
Для обозначения предела функци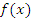и при 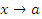используется символическое выражение
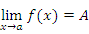
или запись вида
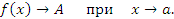
Другими словами, функция 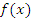имеет своим пределом число A при 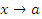, если разность 
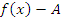представляет собой бесконечно малую функцию 
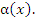Пусть, например,
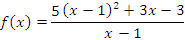
и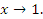 
Тогда из тождества
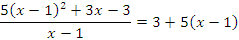
вытекает, что
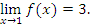
Отметим, что для существования предела функции при 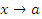не требуется, чтобы эта функция была определена в точке a. Например, функция 
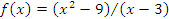не определена в точке x = 3, однако ее предел при 
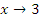существует и равен числу 6. Кроме того, определяющее значение для существования предела функции при 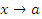имеет только поведение этой функции в достаточно малой окрестности точки a. Вне этой окрестности функция может быть неограниченной. Примером может служить функция f(x) = 1⁄x, предел которой при x → 1 равен 1, хотя эта функция является неограниченной на промежутке, включающем в себя точку 0.
Функция 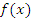называется бесконечно большой при 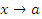, если она неограниченно возрастает по абсолютной величине при 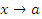. В таких случаях говорят, что 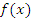стремится к бесконечности при 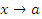и записывают это утверждение в виде
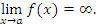
На формальном языке определение предела функци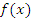и при 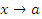выглядит следующим образом. Функция 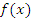имеет своим пределом бесконечность при 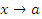, если для любого сколь угодно большого числа E > 0 существует такое число δ(E), что для всех x, удовлетворяющих условию
,
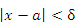выполняется неравенство
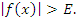
По сути дела такому определению можно дать стандартное толкование: если для всех x из δ-окрестности точки a значения функции 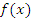попадают в окрестность бесконечно удаленной точки, то при 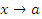эта функции имеет своим пределом ∞.
Аналогичным образом формулируется понятие предела функци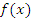и при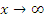 
. Число A называется пределом функци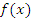и при 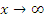, если для любого произвольно малого числа ε > 0 существует такое число ∆(ε), что для всех x, удовлетворяющих условию
 |
(13) |
выполняется неравенство
|
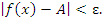(14) |
Функция 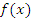имеет своим пределом бесконечность при 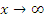, если для любого сколь угодно большого числа E > 0 существует такое число ∆(E), что для всех x, удовлетворяющих условию
выполняется неравенство
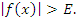
Такой предел обозначается выражением вида
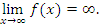
Отметим, что следует соблюдать определенную осторожность при обращении с символом ∞. Порой решающее значение на результат оказывает знак бесконечности. Например,
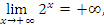
тогда как
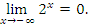
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13