Меню сайта

Категории раздела

Наш опрос

Статистика

Онлайн всего: 1

Гостей: 1

Пользователей: 0

Сравнение бесконечно больших

Раздел 9. Начала математического анализа

Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции

Предел функции

Бесконечно малые функции

Свойства бесконечно малых функций

Предел функции

Свойства пределов функций

Сравнение бесконечно малых

Сравнение бесконечно больших

Первый замечательный предел

Второй замечательный предел

Другие важные пределы: Теорема 3

Другие важные пределы: Теорема 4

Другие важные пределы: Теорема 5

Различные формы неопределенностей

Таблица эквивалентных бесконечно малых

Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13

сравнение бесконечно больших

Сравнение бесконечно больших

Пусть и – бесконечно большие функции при x → a. Рассмотрим возможные значения предела отношения этих функций:

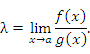
Если 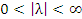, то функции и называются бесконечно большими одного и того же порядка.

Функции и называются эквивалентными бесконечно большими при x → a, если λ = 1. Для записи эквивалентности функций используется обозначение вида

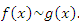
      Функция  называется бесконечно большой более высокого порядка по сравнению с  при x → a, если λ = ∞; при этом говорят, что  имеет меньший порядок роста.

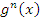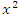      Если  и    представляют собой бесконечно большие функции одного и того же порядка, то функция  называется бесконечно большой n-го порядка по сравнению с . Например, функция    является бесконечно большой 4-го порядка по сравнению с  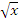  при x → ∞.

      Если λ = 0, то бесконечно большие функции  и  меняются своими ролями. В этом случае функция  является бесконечно большой более высокого порядка по сравнению с  при x → a.

Свойства эквивалентных бесконечно больших функций.

Если и – эквивалентные бесконечно большие функции при x → a, то их разность имеет меньший порядок роста.
Действительно,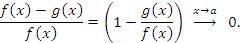
Если и – бесконечно большие функции одного и того же порядка при x → a, то и 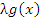являются эквивалентными бесконечно большими функциями:
Иначе говоря, бесконечно большие функци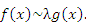и и асимптотически пропорциональны при x → a.
Если бесконечно малая имеет меньший порядок роста по сравнению с при x → a, то

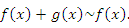
В таких случаях говорят, что – пренебрежимо малая величина по сравнению с .

Примеры:

Бесконечно большие функции и имеют одинаковый порядок роста при x→∞, поскольку предел их отношения равен конечному ненулевому числу:

Если k< n, то любая функция вида есть пренебрежимо малая величина по сравнению с при x → ∞. Например,

Бесконечно большая функция эквивалентна x при x → ∞, поскольку (9x + 7) – пренебрежимо малая величина по сравнению с .
Аналогично, бесконечно большая функция эквивалентна x при x → ∞. Следовательно,

Рассмотрим предел
На первый взгляд представляется разумным заменить эквивалентной функцией 2x. Однако при таком подходе выражение под знаком предела обращается в нуль и, следовательно, (3x + 1) не является пренебрежимо малой величиной. Подобная ситуация характерна для разностей между эквивалентными бесконечно большими величинами и требует определенной аккуратности.

Преобразуем выражение под знаком предела, умножив и разделив его на сопряженное выражение:

Выражение в знаменателе этой дроби представляет собой сумму бесконечно больших функций и поэтому можно заменить эквивалентной величиной 2x, что влечет