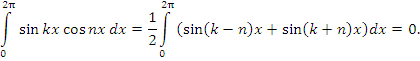Раздел 10. Интеграл и его применение
Тема 10.2 Определенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Ортогональные функции
Функции f(x) и g(x) называются ортогональными на промежутке [a,b], если
 |
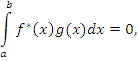(1) |
где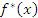 
– функция, комплексно сопряженная f(x).
Если функции f(x) и g(x) являются вещественными, то условие их ортогональности на промежутке [a,b] имеет вид
 |
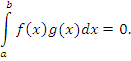(2) |
Ортогональные функции имеют важное значение в теории рядов Фурье, в теории линейных операторов и в других разделах математики и квантовой физики.
Примеры ортогональных функций.
- Пусть
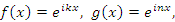где i – мнимая единица; k и n – целые числа.
Ортогональность этих функций на промежутке [0,2π] при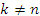
проверяется непосредственным интегрированием:
Учитывая периодичность функций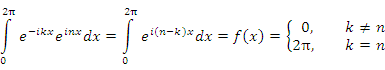
и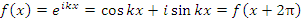
заключаем, что рассматриваемые функции ортогональны на любом промежутке длиной 2π.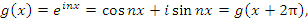
- Функци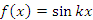и
и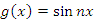 
являются ортогональными на любом промежутке длиной 2π (при ).
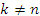Действительно,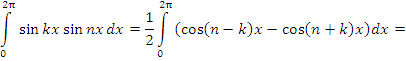
-
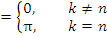
- Свойством ортогональности на промежутке длиной 2π обладают пары функций
при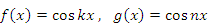
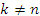, а также
при любых целых значениях k и n: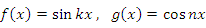
-
-
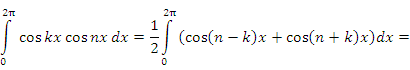
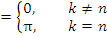
