Раздел 10. Интеграл и его применение
Тема 10.2 Определенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11

Интегрирование периодических функций
Теорема. Пусть f(x) – интегрируемая на промежутке [0,T] периодическая функция с периодом T:
| f(x + T) = f(x). | (1) |
Тогда интеграл
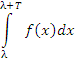 |
(2) |
не зависит от λ. В частности,
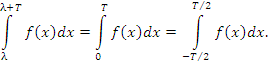 |
(3) |
Доказательство 1. Представим рассматриваемый интеграл в виде суммы трех интегралов:
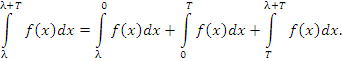 |
(4) |
Вычислим производную по λ от выражения в правой части этого равенства:
|
|
(5) |
Таким образом,
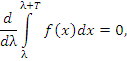 |
(6) |
что и требовалось доказать.
Доказательство 2. Представим рассматриваемый интеграл в виде суммы (4) и преобразуем последний интеграл в правой части, выполнив замену переменной x = t + T. Очевидно, что этот интеграл лишь знаком отличается от первого интеграла в правой части равенства (4):
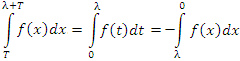 |
(7) |
| Пример 1. Пусть f(x) - периодическая функция с периодом 2π:
Решение. В соответствии с теоремой можно изменить пределы интегрирования периодических функций:
|
| Пример 2. Пусть f(z) - непрерывная на промежутке [0, 1] функция. Показать, что
Решение. Выполним подстановку  : :
|

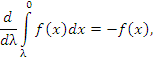
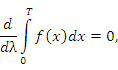
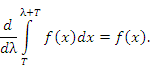





 в симметричных пределах равен удвоенному интегралу по половинному промежутку;
в симметричных пределах равен удвоенному интегралу по половинному промежутку;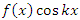 в симметричных пределах равен нулю.
в симметричных пределах равен нулю.


