Площадь плоской фигуры
Раздел 10. Интеграл и его применение
Тема 10.2 Определенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Площадь плоской фигуры
Рассмотрим задачу о вычислении площади фигуры, изображенной на рисунке 1.
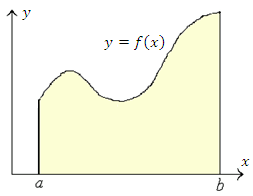
Рис. 1. Криволинейная трапеция, ограниченная графиком функции y = f(x), осью 0x и вертикальными прямыми x = a, x = b.
Разобьем интервал [a,b] на n элементов 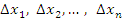 и проведем через точки деления вертикальные линии, разделяя область криволинейной трапеции на ряд полос.
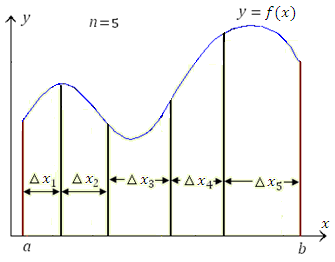
Рис. 2. Разбиение криволинейной трапеции на вертикальные полосы. Промежуток [a,b] разделен на пять частей, чтобы ступеньки были хорошо видны.
Заменим теперь криволинейную фигуру ступенчатой фигурой, образованной прямоугольниками, основание каждого из которых совпадает с основанием соответствующей полосы, а в качестве высоты выступает наименьшая ордината графика функции y = f(x) (см. рисунок 3).
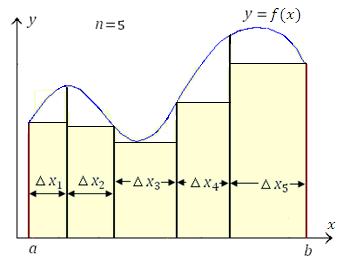
Рис. 3. Аппроксимация криволинейной трапеции ступенчатой фигурой, составленной из прямоугольников, высоты которых равны наименьшим значениям функции f(x) на соответствующих промежутках.
Сумма площадей прямоугольников, изображенных на рисунке 3, дает нижнюю границу площади S криволинейной трапеции:
| |
 |
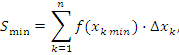(1) |
|
где 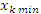 – точка с наименьшим значением функции f(x) на промежутке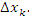 
Сумма 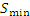 называется нижней интегральной суммой или нижней суммой Дарбу.
Аналогичным образом можно сформировать ступенчатую фигуру, высоты прямоугольников которой равны наибольшим ординатам графика функции y = f(x) в пределах соответствующих полос.
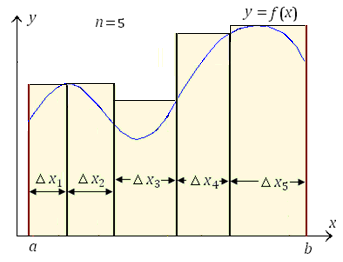
Рис. 4. Аппроксимация криволинейной трапеции ступенчатой фигурой, составленной из прямоугольников, высоты которых равны наибольшим значениям функции f(x) на соответствующих промежутках.
Верхняя граница площади криволинейной трапеции описывается формулой
| |
 |
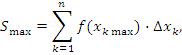(2) |
|
где 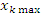 – точка с наибольшим значением функции f(x) на промежутке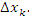
Сумма 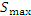 называется верхней интегральной суммой или верхней суммой Дарбу. Очевидно, что
| |
 |
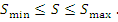(3) |
|
С увеличением числа элементов разбиения интервала [a,b] суммы Дарбу 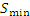и 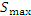более точно аппроксимирует площадь криволинейной трапеции, ограниченной сверху кривой y = f(x) , снизу – осью 0x, а с боков – вертикальными отрезками прямых x = a и x = b. При безграничном убывании всех 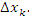разность между наименьшим и наибольшим значениями функции f(x) на каждом промежутке 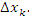стремится к нулю и, следовательно,
| |
 |
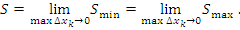(4) |
|
Другими словами, выбор точки 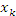 на промежутке  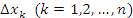не оказывает влияния на конечный результат. Таким образом,
| |
 |
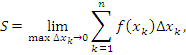(5) |
|
где 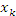– произвольная точка промежутка 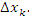Предельное значение суммы вида (5) обозначаются символическим выражением
| |
 |
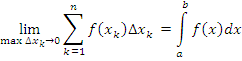(6) |
|
и называется определенным интегралом от функции f(x) по промежутку [a,b]. (Читается: “Интеграл от эф от икс по икс от а до бэ”.)
Если существует предел (6), то говорят, что функция f(x) является интегрируемой на промежутке [a,b]. При этом величины a и b называют соответственно нижним и верхним пределами интегрирования.
Согласно вышеизложенному, определенный интеграл от положительно определенной функции f(x) по промежутку [a,b] может интерпретироваться как площадь плоской фигуры, образованной графиком функции y = f(x), отрезком [a,b] и вертикальными отрезками прямых x = a и x = b (которые могут вырождаться в точки).
Если на некотором промежутке график функции y = f(x) расположен ниже оси 0x, то интеграл на этом промежутке принимает отрицательное значение.
Рис. 5. Интеграл по промежутку, на котором подынтегральная функция принимает как положительные так и отрицательные значения.
(Для смены изображения подведите курсор к области рисунка.)
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
|
