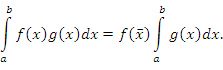Раздел 10. Интеграл и его применение

Тема 10.2 Определенные интегралы

Площадь плоской фигуры

Движение частицы с переменной скоростью

Понятие определенного интеграла

Классы интегрируемых функций

Свойства определенных интегралов

Формула Ньютона–Лейбница

Интегрирование заменой переменной

Интегрирование по частям

Интегрирование четных и нечетных функций

Интегрирование периодических функций

Ортогональные функции

Страницы:  1  | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11

Свойства определенных интегралов

1. Интеграл от единицы по промежутку [a,b] равен длине этого промежутка:

   

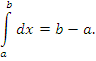
2. Интеграл не зависит от символа, используемого для обозначения переменной интегрирования:

   

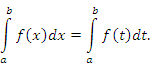
3. Постоянный множитель можно выносить за знак интеграла:

   

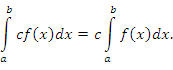
4. Интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме интегралов:

   

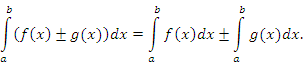
5. При перестановке местами пределов интегрирования интеграл меняет свой знак на противоположный:

   

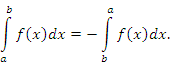
6. Если нижний и верхний пределы интегрирования совпадают между собой, то интеграл равен нулю:

   

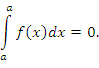
7. Если функция  f(x)  интегрируема на каждом из промежутков  [a,b],  [a,c]  и  [c,b], то

   

   Это свойство вполне очевидно, если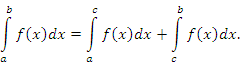 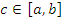 (см. рисунок 1).

    
    

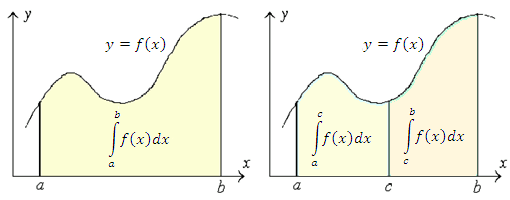
8. Рис. 1. Свойство 6 (случай ).

   
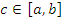   Однако оно остается справедливым и в том случае, когда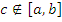  – при условии, что существуют интегралы  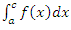и :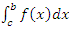

    
    

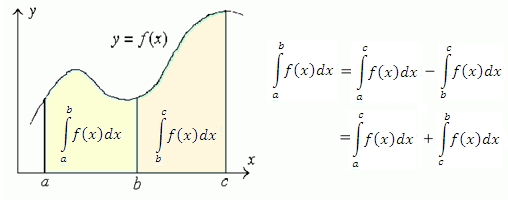
Рис. 2. Свойство 6 (случай ).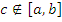

1. Если функция  f(x)  является положительно определенной и интегрируемой на промежутке [a,b], то

   

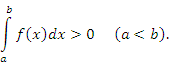
2. Пусть функции  f(x)  и  g(x)  интегрируемы на промежутке [a,b] и 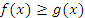 во всех точках этого промежутка. Тогда

   

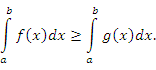
3. Если функция  f(x)  интегрируема на промежутке [a,b], то

   

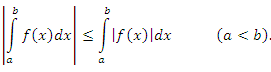
4. Пусть функция  f(x)  интегрируема на промежутке [a,b] и удовлетворяет неравенствам 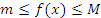 во всех точках этого промежутка. Тогда

   

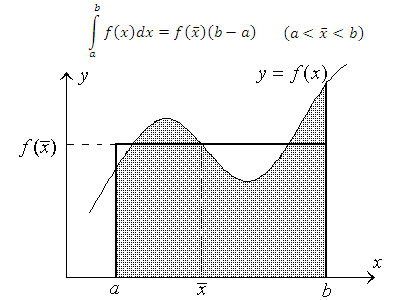
   Выражение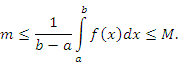 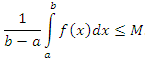называется средним значением функции  f(x)  на промежутке [a,b]. Поэтому свойство 8 называют теоремой о среднем.
5. Теорема о среднем для непрерывной функции. Пусть функция  f(x)  непрерывна и ограничена на промежутке [a,b]. Тогда на этом промежутке найдется такая "средняя" точка 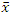, что

   
    

6. 
    
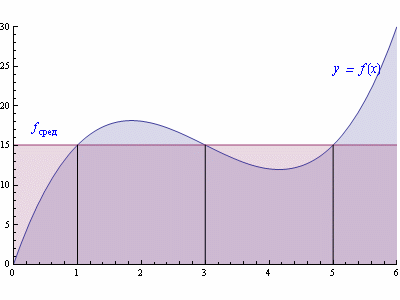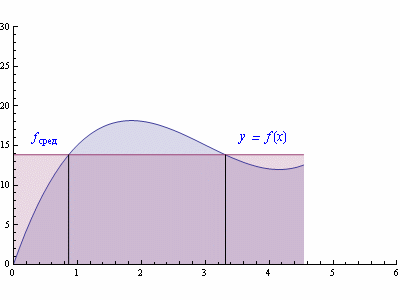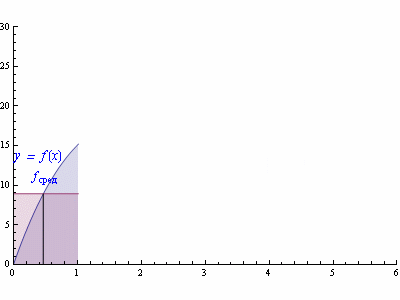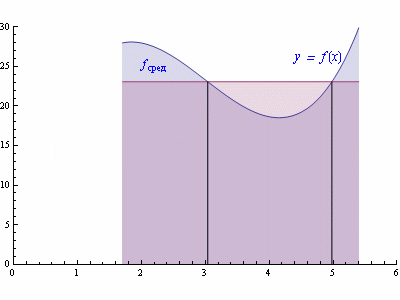
   Рис. 3. Площадь под кривой  y = f(x)  на интервале [a,b] равна площади прямоугольника с основанием (b-a) и высотой .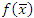 
   Для просмотра анимации в других цветах подведите курсор указателя мыши в область рисунка, расположенного справа.

7. Обобщенная теорема о среднем. Пусть функции  f(x)  и  g(x)  интегрируемы на промежутке [a,b]. Если при этом функция  f(x)  является непрерывной, то на этом промежутке найдется такая "средняя" точка 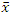, что

   

Страницы:  1  | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11