Раздел 10. Интеграл и его применение
Тема 10.2 Определенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Движение частицы с переменной скоростью
Рассмотрим задачу о вычислении перемещения s частицы за промежуток времени от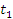 
до 
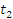при движении частицы вдоль некоторой прямой с переменной скоростью 
.
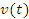Разобьем промежуток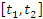 
на столь малые интервалы 
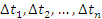, чтобы изменением скорости частицы в пределах каждого интервала можно было пренебречь.
Пусть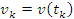 
– скорость частицы на промежутке времени 
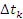. Тогда перемещение 
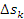частицы за время 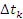можно найти по формуле 
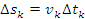. Перемещение s представляет собой сумму перемещений :
 |
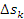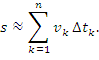(1) |
Равенство (1) является приближенным, поскольку скорость частицы несколько изменяется за время 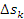. Точность этой формулы возрастает, если интервал 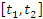разбивать на все меньшие элементы, увеличивая тем самым число элементов. Выполнив предельный переход 
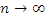и все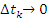 
, получаем точную формулу для перемещения частицы за промежуток времени от 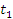до :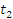
 |
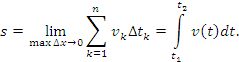(2) |
Если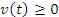 
на промежутке 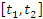, то перемещение частицы равно по величине пройденному ее пути и – в соответствии с геометрической интерпретацией определенного интеграла – численно совпадает с площадью области, расположенной под графиком функции 
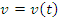на этом промежутке.
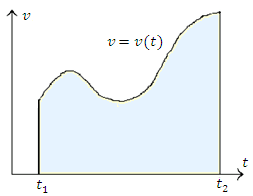
Рис. 1. Путь, пройденный частицей, равен площади области, расположенной под графиком скорости движения.