Раздел 10. Интеграл и его применение
Тема 10.2 Определенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Интегрирование заменой переменной
Теорема. Пусть функция f(x) является непрерывной на промежутке [a,b] относительно переменной x, которая в свою очередь является функцией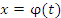 
переменной t на промежутке 
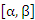и имеет на нем непрерывную производную. Если 
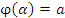и 
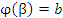, то
 |
(1) |
Доказательство. Используя формулу Ньютона–Лейбница, определение первообразной и учитывая условия теоремы, получаем
|
|
(2) |
