Раздел 10. Интеграл и его применение
Тема 10.1 Неопределенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Замена переменной
Если произвольным образом задать функцию, то в подавляющем большинстве случаев интеграл от такой функции будет неберущимся - в том смысле, что не существует какой-либо конечной комбинации элементарных функций, производная от которой равнялась бы этой функции.
Некоторым таким неберущимся интегралам присваивают персональные имена и называют их специальными функциями. Из соображений удобства подстановки можно подразделить на два типа: 1)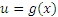 
; 2) 
.
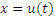В обоих случаях речь идет о замене переменной, а различие заключается только в технике реализации этой замены.
- Подстановка 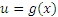применяется для преобразования подынтегрального выражения, например, в интегралах вида
Учитывая равенство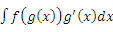
.(1)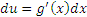 
, получаем более простой интеграл
- по крайней мере, судя по его внешнему виду.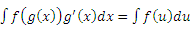
(2) 
- Подстановка x = u(t) используется для преобразования интеграла
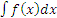к другому виду:
 . |
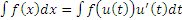(3) |
Возможно, что интеграл в правой части этого равенства окажется более простым, чем исходный. Иначе следует подумать о других подстановках или же применить другой метод интегрирования.
Умение применять "хорошие" подстановки совершенствуется по мере развития навыков вычисления интегралов. Однако во многих случаях разумная замена переменной бывает просто очевидной. В качестве примера проанализируем интеграл
 |
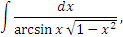(4) |
под знаком которого содержится обратная тригонометрическая функция и одновременно – иррациональное выражение. В подобных случаях, как правило, возможны всего два варианта: либо интеграл вычисляется элементарно, либо является неберущимся. Среди табличных интегралов нет ни одного, содержащего арксинус (к тому же еще и в знаменателе). Уже этого обстоятельства достаточно для того, чтобы испытать подстановку 
, которая влечет 
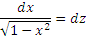и, следовательно,
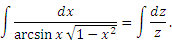
Подстановка была вынужденной, но оказалась удачной: интеграл приведен к табличному виду. Все оказалось внутренне согласованным – нужный радикал в нужном месте в комбинации с нужной функцией. Достаточно, например, заменить единицу под знаком корня на любое другое число или же изменить степень корня, чтобы превратить интеграл в не берущийся. Так, любой из нижеприведенных интегралов является неберущимся:
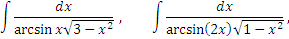
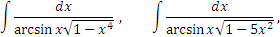
Обсудим другой прием, позволяющий непосредственным образом выйти на разумную подстановку. Обратимся вновь к интегралу (4) и представим подынтегральное выражение в виде
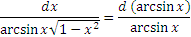
Теперь переменная x входит только под знак арксинуса и последующие действмя представляются вполне очевидными. В таких случаях говорят, что мы "подвели множитель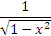 
под знак дифференциала".
Другие примеры:
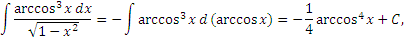
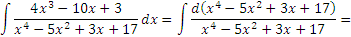
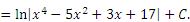
Пример 1. Для вычисления интеграла  выполним замену переменной: t = ln x. Тогда
|
| Пример 2.
|
(замена 
)| Пример 3.
|
(замена 
)| Пример 4.
|
(замена 
)| Пример 5.
|
(замена | Пример 6.
|
(замена 
)