Раздел 10. Интеграл и его применение
Тема 10.1 Неопределенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Свойства первообразной
Пусть функция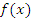 
определена на некотором промежутке D. Функция 
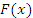называется первообразной функции 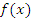, если
 |
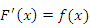(1) |
для всех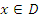 
.
Если к первообразной 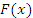функции 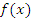прибавить любую постоянную C, то полученная функция 
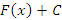также является первообразной, поскольку
 |
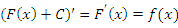(2) |
Справедливо и более сильное утверждение:
Любые две первообразные одной и той же функции отличаются друг от друга не более чем на постоянную величину C.
Действительно, пусть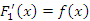 
и 
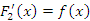для всех .
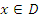Тогда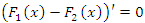 
и, следовательно, разность 
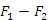есть величина постоянная:
 |
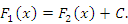(3) |
Примеры:
| Пример 1. Функция 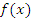является первообразной для  . |
| Пример 2. Обе функции,  и 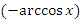 , являются первообразными для функции  на промежутке  .Следовательно, их разность равна некоторой постоянной:
Выражение в левой части этого равенства обращается в  при x = 0. Таким образом,
|
| Пример 3. Аналогичные рассуждения относительно первообразных функции  приводят к формуле
|
