Раздел 10. Интеграл и его применение
Тема 10.1 Неопределенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Обобщение таблицы интегралов
Согласно одному из свойств неопределенных интегралов, равенство
 |
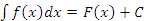(1) |
остается неизменным при замене переменной интегрирования некоторой дифференцируемой функцией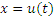 
:
 |
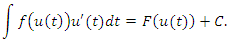(2) |
Поэтому каждый табличный интеграл можно рассматривать с более общих позиций, подставляя вместо переменной интегрирования различные функции 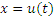. Такой подход позволяет расширить таблицу интегралов и оказывается конструктивным при составлении задач.
Разъясним эти соображения на примере интеграла от степенной функции,
 |
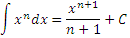(3) |
Выполнив постановку 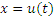, получаем новую формулу,
 |
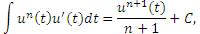(4) |
устанавливающую более общее правило интегрирования.
В качестве функции 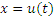может выступать любая функция, имеющая на соответствующем промежутке непрерывную производную.
Пусть, в частности, n = 3 и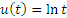 
. Тогда
 |
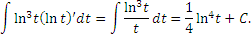(5) |
Аналогично, при n = 2 и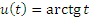 
имеем
 |
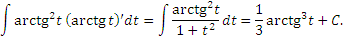(6) |
Подобным образом можно интерпретировать другие интегралы, заменяя переменную интегрирования той или иной функцией.
| Пример 1.
|
| Пример 2.
|
| Пример 3.
|
| Пример 4.
|
| Пример 5.
|
