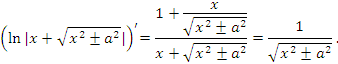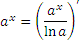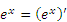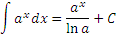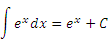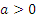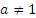Раздел 10. Интеграл и его применение
Тема 10.1 Неопределенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11

Таблица простейших интегралов
Возьмем за основу таблицу основных производных и представим каждую формулу вида 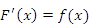 равносильным интегральным равенством
равносильным интегральным равенством 
- Рассмотрим правило дифференцирования степенной функции:
Разделим обе части этого равенства на (n + 1) и внесем постоянный множитель под знак производной: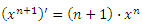
(1)
Функция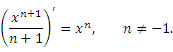
(2) 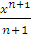 является первообразной для
является первообразной для 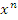 и, следовательно,
и, следовательно,
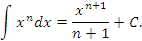
(3) - Функция
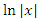 является первообразной для функции
является первообразной для функции 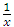 при любых
при любых 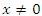 .
.
Действительно, пусть x > 0. Тогда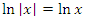 и
и 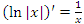 .
.
Если x < 0, то и
и 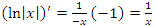 .
.
Следовательно,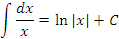
(4)
Аналогичным образом можно преобразовать другие формулы дифференциального исчисления. В результате мы получаем следующую таблицу.
| N | Дифференциальная форма | Интегральная форма | Условия |
|---|---|---|---|
| 1 | 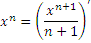 |
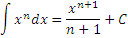 |
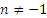 |
| 2 | 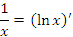 |
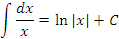 |
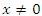 |
| 3 |
|
|
|
| 4 | 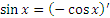 |
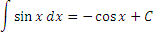 |
|
| 5 | 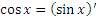 |
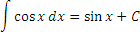 |
|
| 6 | 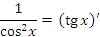 |
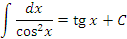 |
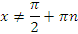 |
| 7 | 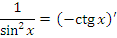 |
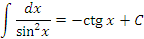 |
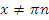 |
| 8 | 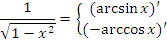 |
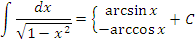 |
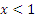 |
| 9 | 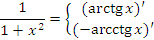 |
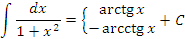 |
|
| 10 | 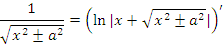 |
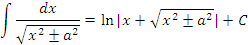 |
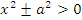 |
Справедливость представленных в таблице интегральных формул легко проверяется непосредственным дифференцированием. В частности,