Раздел 10. Интеграл и его применение
Тема 10.1 Неопределенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Методы интегрирования
Чтобы продифференцировать какую-либо функцию, достаточно следовать простым правилам. При этом вид дифференцируемой функции практически несущественен – с точки зрения самой возможности получения результата.
Совсем не так обстоит дело с интегрированием функций. Например, легко продифференцировать функцию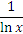 
, однако интеграл от этой функции является неберущимся – в том смысле, что его нельзя представить в виде конечной комбинации элементарных функций.
Не существует универсального рецепта, пригодного для интегрирования любой функции. В каких-то случаях достаточно выполнить простые преобразования подынтегрального выражения или же разложить интегрируемую дробь на сумму простых дробей. Например, для интегрирования функции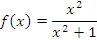 
достаточно представить ее в виде 
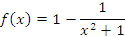и воспользоваться свойством интеграла от разности функций.
В более сложных случаях требуется использование иных приемов, характер которых определяется типом интегрируемой функции. При этом на передний план выходит классификация интегралов по различного вида признакам.
К наиболее важным методам интегрирования относятся
- метод замены переменной (другое название которого – метод подстановки);
- метод интегрирования по частям.
Конечной целью применения методов интегрирования – за редкими исключениями – является сведение данного интеграла к табличному виду.