Раздел 10. Интеграл и его применение
Тема 10.1 Неопределенные интегралы
Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11
Свойства неопределенных интегралов
Напомним, что по определению
|
|
(1) |
.
Отсюда вытекают следующие свойства.
- Интегрирование и дифференцирование являются взаимно обратными операциями:
(2) 
(3) 
(4) - Постоянный множитель можно выносить за знак интеграла:
Действительно,
(5) 
и, следовательно, функция 
является первообразной для 
. - Если функции
и 
интегрируемы на некотором промежутке, то на этом промежутке интегрируема и их сумма (разность). При этом интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:
. |
(6) |
Для доказательства достаточно убедиться в том, что выражение в правой части этого равенства является первообразной для функции 
:
4. Пусть 
. Тогда для любой непрерывно дифференцируемой функции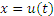 
выполняется равенство
 |
(7) |
Это свойство основывается на инвариантности формы первого дифференциала, согласно которому дифференциал 
сохраняет свою форму при замене независимой переменной на функцию другой переменной: 
.
В случае удачной замены переменной можно получить более простую для интегрирования функцию. Например, выражение 
преобразуется заменой переменной 
к виду 
и, следовательно,
| Пример 1.
|
| Пример 2.
|
| Пример 3.
|
| Пример 4.
|
| Пример 5.
|
| Пример 6.
|
| Пример 7.
|
