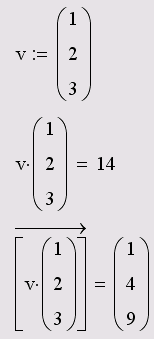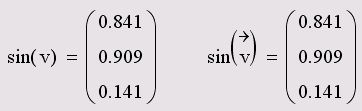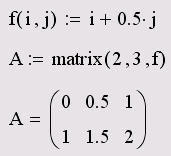Векторная алгебра Mathcad включает несколько необычный оператор, который называется оператором векторизации (vectorize operator). Этот оператор предназначен, как правило, для работы с массивами. Он позволяет провести однотипную операцию над всеми элементами массива (т. е. матрицы или вектора), упрощая тем самым программирование циклов. Например, иногда требуется умножить каждый элемент одного вектора на соответствующий элемент другого вектора. Непосредственно такой операции в Mathcad нет, но ее легко осуществить с помощью векторизации (листинг 23.15). Для этого:
Введите векторное выражение, как показано во второй строчке листинга (обратите внимание, что в таком виде символ умножения обозначает оператор скалярного произведения векторов).
Переместите курсор таким образом, чтобы линии ввода выделяли все выражение, которое требуется подвергнуть векторизации (рис. 23.2).
Введите оператор векторизации, нажав кнопку Vectorize (Векторизация) на панели Matrix (Матрица) (рис. 23.2), или сочетанием клавиш +<->.
Введите <=>, чтобы получить результат.
Рис. 23.2. Оператор векторизации
Листинг 23.15. Использование векторизации для перемножения элементов вектора
Оператор векторизации можно использовать только с векторами и матрицами одинакового размера. Большинство неспецифических функций Mathcad не требуют векторизации для проведения одной и той же операции над всеми элементами вектора. Например, аргументом тригонометрических функций по определению является скаляр. Если попытаться вычислить синус векторной величины, Mathcad осуществит векторизацию по умолчанию, вычислив синус каждого элемента и выдав в качестве результата соответствующий вектор. Пример показан в листинге 23.16.
Листинг 23.16. Векторизация необязательна для большинства функций Mathcad
Все матричные и векторные операторы, о которых шла речь выше, допустимо использовать в символьных вычислениях. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными. Несколько примеров приведены в листинге 23.17.
Листинг 23.17. Примеры символьных операций над векторами и матрицами
Смело используйте символьный процессор в качестве мощного математического справочника. Например, когда Вы хотите вспомнить какое-либо определение из области линейной алгебры (так, правила перемножения и обращения матриц показаны в первых строках листинга 23.17).
Перечислим основные встроенные функции, предназначенные для облегчения работы с векторами и матрицами. Они нужны для создания матриц, слияния и выделения части матриц, получения основных свойств матриц и т.п.
Самым наглядным способом создания матрицы или вектора является применение первой кнопки панели инструментов Matrix (Матрицы). Однако в большинстве случаев, в частности при программировании сложных проектов, удобнее бывает создавать массивы с помощью встроенных функций. Определение элементов матрицы через функцию matrix(M,N,f) — создание матрицы размера MXN, каждый i,j элемент которой есть f (i, j) (листинг 23.18); м — количество строк; N — количество столбцов; f (i, j) — функция.
Листинг 23.18. Создание матрицы
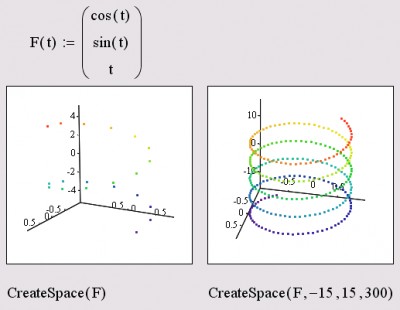
Для создания матриц имеются еще две специфические функции, применяемые, в основном, для быстрого и эффектного представления каких-либо зависимостей в виде трехмерных графиков (типа поверхности или пространственной кривой). Все их аргументы, кроме первого (функции), необязательны. Рассмотрим первую из функций.
F(t) — векторная функция из трех элементов, заданная параметрически относительно единственного аргумента t; f1(t) ,f2(t), f3(t) — скалярные функции;
t0 — нижний предел t (по умолчанию -5); t1 — верхний предел t (по умолчанию 5);
tgrid — число точек сетки по переменной t (по умолчанию 2о);
fmap — векторная функция от трех аргументов, задающая преобразование координат.
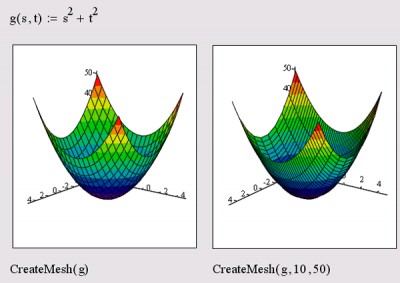
Рис. 23.3. Использование функции CreateSpace с разным набором параметров
Пример использования функции CreateSpace показан на рис. 23.3. Заметьте, для построения графика спирали не потребовалось никакого дополнительного кода, кроме определения параметрической зависимости в вектор-функции F!
Функция создания матрицы для графика трехмерной поверхности устроена совершенно аналогично, за тем исключением, что для определения поверхности требуется не одна, а две переменных. Пример ее использования иллюстрирует рис. 23.4.
Рис. 23.4. Использование функции CreateMesh с разным набором параметров
CreateMesh(F(или g, или f1, f2, f3) , s0, s1, t0, t1, sgrid, tgrid, fmap) - создание вложенного массива, представляющего х-, у- и z-координаты параметрической поверхности, заданной функцией F:
F(s,t) — векторная функция из трех элементов, заданная параметрически относительно двух аргументов s и t; g (s, t) — скалярная функция;
f1(s,t),f2(s,t),f3(s,t) — скалярные функции;
s0, t0 — нижние пределы аргументов s, t (по умолчанию -5);
s1, t1 — верхние пределы аргументов s, t (по умолчанию 5);
sgrid, tgrid — число точек сетки по переменным s и t (по умолчанию 20);
fmap — векторная функция из трех элементов от трех аргументов, задающая преобразование координат.
Примеры вложенных массивов, которые создаются функциями createMesh и createspace, приведены в листинге 23.19. Каждая матрица из числа трех вложенных матриц, образующих массив, определяет х-, у- и z-координаты точек поверхности или кривой, соответственно.
Листинг 23.19. Результат действия функций CreateMeeh и CreateSpace (рис. 23.3 - 23.4)
Создание матриц специального вида В Mathcad легко создать матрицы определенного вида с помощью одной из встроенных функций. Примеры использования этих функций приведены в листинге 23.20.
identity (N) — единичная матрица размера NXN;
diag(v) — диагональная матрица, на диагонали которой находятся элементы вектора v;
geninv(A) — создание матрицы, обратной (слева) матрице А;
rref (A) — преобразование матрицы или вектора А в ступенчатый вид;
N — целое число;
v — вектор; А —матрица из действительных чисел.
Размер NXM матрицы А для функции geninv должен быть таким, чтобы N>M.
