Обзор программ для символьной математики
Символьная, или, как еще говорят, компьютерная, математика либо компьютерная алгебра, — большой раздел математического моделирования. В принципе, программы такого рода можно отнести к инженерным программам автоматизированного проектирования. Таким образом, в области инженерного проектирования выделяют три основных раздела:
- CAD — Computer Aided Design;
- CAM — Computer Aided Manufacturing;
- CAE — Computer Aided Engeneering.
Сегодня серьезное конструирование, градостроительство и архитектура, электротехника и масса смежных с ними отраслей, а также учебные заведения технической направленности уже не могут обойтись без систем автоматизированного проектирования (САПР), производства и расчетов. А математические пакеты являются составной частью мира CAE-систем, но эта часть никак не может считаться второстепенной, поскольку некоторые задачи вообще невозможно решить без помощи компьютера. Более того, к системам символьной математики сегодня прибегают даже теоретики (так называемые чистые, а не прикладные математики), например для проверки своих гипотез.
Всего каких-нибудь 15 лет назад эти системы считались сугубо профессиональными, но середина 90-х годов стала переломным моментом для мирового рынка CAD/CAM/CAE-систем массового применения. Тогда, впервые за долгое время, пакеты для параметрического моделирования с промышленными возможностями стали доступны пользователям персональных компьютеров. Создатели подобных систем учли требования широкого круга пользователей и таким образом дали возможность десяткам тысяч инженеров и математиков использовать на своих персональных рабочих местах новейшие достижения науки в области технологий CAD/CAM/CAE-систем.
Так что же умеют программы математического моделирования? Неужели они требуют от ученых умения программировать на тех или иных алгоритмических языках, отлаживать программы, отлавливать ошибки и тратить массу времени на получение результата? Нет, те времена давно прошли, и теперь в математических пакетах применяется принцип конструирования модели, а не традиционное «искусство программирования». То есть пользователь лишь ставит задачу, а методы и алгоритмы решения система находит сама. Более того, такие рутинные операции, как раскрывание скобок, преобразование выражений, нахождение корней уравнений, производных и неопределенных интегралов компьютер самостоятельно осуществляет в символьном виде, причем практически без вмешательства пользователя.
Современные математические пакеты можно использовать и как обычный калькулятор, и как средства для упрощения выражений при решении каких-либо задач, и как генератор графики или даже звука! Стандартными стали также средства взаимодействия с Интернетом, и генерация HTML-страниц выполняется теперь прямо в процессе вычислений. Теперь можно решать задачу и одновременно публиковать для коллег ход ее решения на своей домашней странице.
Рассказывать о программах математического моделирования и возможных областях их применения можно очень долго, но мы ограничимся лишь кратким обзором ведущих программ, укажем их общие черты и различия. В настоящее время практически все современные CAE-программы имеют встроенные функции символьных вычислений. Однако наиболее известными и приспособленными для математических символьных вычислений считаются Maple, MathCad, Mathematica и MatLab. Но, делая обзор основных программ символьной математики, мы укажем и на возможные альтернативы, идеологически схожие с тем или иным пакетом-лидером.
Так что же делают эти программы и как они помогают математикам? Основу курса математического анализа в высшей школе составляют такие понятия, как пределы, производные, первообразные функций, интегралы разных видов, ряды и дифференциальные уравнения. Тому, кто знаком с основами высшей математики, наверняка известны десятки правил нахождения пределов, взятия интегралов, нахождения производных и т.д. Если добавить к этому то, что для нахождения большинства интегралов нужно также помнить таблицу основных интегралов, то получается поистине огромный объем информации. И если какое-то время не тренироваться в решений подобных задач, то многое быстро забывается и для нахождения, например, интеграла посложнее придется уже заглядывать в справочники. Но ведь взятие интегралов и нахождение пределов в реальной работе не является главной целью вычислений. Реальная цель заключается в решении каких-либо проблем, а вычисления — всего лишь промежуточный этап на пути к этому решению.
С помощью описываемого ПО можно сэкономить массу времени и избежать многих ошибок при вычислениях. Естественно, CAE-системы не ограничиваются только этими возможностями, но в данном обзоре мы сделаем упор именно на них.
Отметим только, что спектр задач, решаемых подобными системами, очень широк:
- проведение математических исследований, требующих вычислений и аналитических выкладок;
- разработка и анализ алгоритмов;
- математическое моделирование и компьютерный эксперимент;
- анализ и обработка данных;
- визуализация, научная и инженерная графика;
- разработка графических и расчетных приложений.
При этом отметим, что поскольку CAE-системы содержат операторы для базовых вычислений, то почти все алгоритмы, отсутствующие в стандартных функциях, можно реализовать посредством написания собственной программы.
MatLab (http://www.mathworks.com/)
Минимальные требования к системе:
- процессор Pentium III, 4, Xeon, Pentium M; AMD Athlon, Athlon XP, Athlon MP;
- 256 Мбайт оперативной памяти (рекомендуется 512 Мбайт);
- 400 Мбайт дискового пространства (только для самой системы MatLab и ее Help);
- операционная система Microsoft Windows 2000 (SP3)/XP.
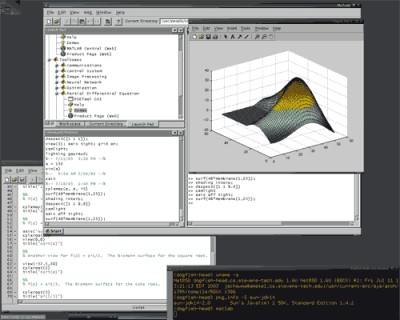
Рис. 20.1. Интерфейс системы MatLab
Система MatLab относится к среднему уровню продуктов, предназначенных для символьной математики, но рассчитана на широкое применение в сфере CAE (то есть сильна и в других областях). MatLab — одна из старейших, тщательно проработанных и проверенных временем систем автоматизации математических расчетов, построенная на расширенном представлении и применении матричных операций. Это нашло отражение и в самом названии системы — MATrix LABoratory, то есть матричная лаборатория. Однако синтаксис языка программирования системы продуман настолько тщательно, что данная ориентация почти не ощущается теми пользователями, которых не интересуют непосредственно матричные вычисления.
Несмотря на то что изначально MatLab предназначалась исключительно для вычислений, в процессе эволюции (а сейчас выпущена уже версия 7), в дополнение к прекрасным вычислительным средствам, у фирмы Waterloo Maple по лицензии для MatLab было приобретено ядро символьных преобразований, а также появились библиотеки, которые обеспечивают в MatLab уникальные для математических пакетов функции. Например, широко известная библиотека Simulink, реализуя принцип визуального программирования, позволяет построить логическую схему сложной системы управления из одних только стандартных блоков, не написав при этом ни строчки кода. После конструирования такой схемы можно детально проанализировать ее работу.
В системе MatLab также существуют широкие возможности для программирования. Ее библиотека C Math (компилятор MatLab) является объектной и содержит свыше 300 процедур обработки данных на языке C. Внутри пакета можно использовать как процедуры самой MatLab, так и стандартные процедуры языка C, что делает этот инструмент мощнейшим подспорьем при разработке приложений (используя компилятор C Math, можно встраивать любые процедуры MatLab в готовые приложения).
Библиотека C Math позволяет пользоваться следующими категориями функций:
- операции с матрицами;.
- сравнение матриц;
- решение линейных уравнений;
- разложение операторов и поиск собственных значений;
- нахождение обратной матрицы;
- поиск определителя;
- вычисление матричного экспоненциала;
- элементарная математика;
- функции beta, gamma, erf и эллиптические функции;
- основы статистики и анализа данных;
- поиск корней полиномов;
- фильтрация, свертка;
- быстрое преобразование Фурье (FFT);
- интерполяция;
- операции со строками;
- операции ввода-вывода файлов и т.д.
При этом все библиотеки MatLab отличаются высокой скоростью численных вычислений. Однако матрицы широко применяются не только в таких математических расчетах, как решение задач линейной алгебры и математического моделирования, обсчета статических и динамических систем и объектов. Они являются основой автоматического составления и решения уравнений состояния динамических объектов и систем. Именно универсальность аппарата матричного исчисления значительно повышает интерес к системе MatLab, вобравшей в себя лучшие достижения в области быстрого решения матричных задач. Поэтому MatLab давно уже вышла за рамки специализированной матричной системы, превратившись в одну из наиболее мощных универсальных интегрированных систем компьютерной математики.
Рис. 20.2. Библиотека Image Processing Toolbox системы MatLab
Для визуализации моделирования система MatLab имеет библиотеку Image Processing Toolbox, которая обеспечивает широкий спектр функций, поддерживающих визуализацию проводимых вычислений непосредственно из среды MatLab, увеличение и анализ, а также возможность построения алгоритмов обработки изображений. Усовершенствованные методы графической библиотеки в соединении с языком программирования MatLab обеспечивают открытую расширяемую систему, которая может быть использована для создания специальных приложений, пригодных для обработки графики.
Основные средства библиотеки Image Processing Tollbox:
- построение фильтров, фильтрация и восстановление изображений;
- увеличение изображений;
- анализ и статистическая обработка изображений;
- выделение областей интересов, геометрические и морфологические операции;
- манипуляции с цветом; двумерные преобразования; блок обработки;
- средство визуализации;
- запись/чтение графических файлов.
Таким образом, систему MatLab можно использовать для обработки изображений, сконструировав собственные алгоритмы, которые будут работать с массивами графики как с матрицами данных. Поскольку язык MatLab оптимизирован для работы с матрицами, в результате обеспечивается простота использования, высокая скорость и экономичность проведения операций над изображениями.
Таким образом, программу MatLab можно использовать для восстановления испорченных изображений, шаблонного распознавания объектов на изображениях или же для разработки каких-либо собственных оригинальных алгоритмов обработки изображений. Библиотека Image Processing Tollbox упрощает разработку высокоточных алгоритмов, поскольку каждая из функций, включенных в эту библиотеку, оптимизирована для максимального быстродействия, эффективности и достоверности вычислений. Кроме того, библиотека обеспечивает разработчика многочисленным инструментарием для создания собственных решений и для реализаций сложных приложений обработки графики. А при анализе изображений использование мгновенного доступа к мощным средствам визуализации помогает моментально увидеть эффекты увеличения, восстановления и фильтрации.
Среди других библиотек системы MatLab можно также отметить System Identification Toolbox — набор инструментов для создания математических моделей динамических систем, основанных на наблюдаемых входных/выходных данных. Особенностью этого инструментария является наличие гибкого пользовательского интерфейса, позволяющего организовать данные и модели. Библиотека System Identification Toolbox поддерживает как параметрические, так и непараметрические методы. Интерфейс системы облегчает предварительную обработку данных, работу с итеративным процессом создания моделей для получения оценок и выделения наиболее значимых данных. Быстрое выполнение с минимальными усилиями таких операций, как открытие/сохранение данных, выделение области возможных значений данных, удаление погрешностей, предотвращение ухода данных от характерного для них уровня.
Наборы данных и идентифицируемые модели организуются графически, что позволяет легко вызвать результаты предыдущих анализов в течение процесса идентификации системы и выбрать следующие возможные шаги процесса. Основной пользовательский интерфейс организует данные для показа уже полученного результата. Это облегчает быстрое сравнение по оценкам моделей, позволяет выделять графическими средствами наиболее значимые модели и исследовать их показатели.
А что касается математических вычислений, то MatLab предоставляет доступ к огромному количеству подпрограмм, содержащихся в библиотеке NAG Foundation Library компании Numerical Algorithms Group Ltd (инструментарий имеет сотни функций из различных областей математики, и многие из этих программ были разработаны широко известными в мире специалистами). Это уникальная коллекция реализаций современных численных методов компьютерной математики, созданных за последние три десятка лет. Таким образом, MatLab вобрала и опыт, и правила, и методы математических вычислений, накопленные за тысячи лет развития математики. Одну только прилагаемую к системе обширную документацию вполне можно рассматривать как фундаментальный многотомный электронный справочник по математическому обеспечению.
Из недостатков системы MatLab можно отметить невысокую интегрированность среды (очень много окон, с которыми лучше работать на двух мониторах), не очень внятную справочную систему (а между тем объем фирменной документации достигает почти 5 тыс. страниц, что делает ее трудно обозримой) и специфический редактор кода MatLab-программ. Сегодня система MatLab широко используется в технике, науке и образовании, но все-таки она больше подходит для анализа данных и организации вычислений, нежели для чисто математических выкладок.
Поэтому для проведения аналитических преобразований в MatLab используется ядро символьных преобразований Maple, а из Maple для численных расчетов можно обращаться к MatLab. Ведь недаром символьная математика Maple вошла составной частью в целый ряд современных пакетов, а численный анализ от MatLab и наборы инструментов (Toolboxes) уникальны. Тем не менее математические пакеты Maple и MatLab — это интеллектуальные лидеры в своих классах, это образцы, определяющие развитие компьютерной математики.
| Лекции: Введение | Л-1: Краткая история компьютерной графики. Основные понятия о машинной графике и основные задачи компьютерной графики. Классификация направлений и сферы применения компьютерной графики. Задачи курса | Л-2: Программное обеспечение для создания, просмотра и обработки графической информации | Л-3: Текстовый редактор. Работа с текстом (простой и фигурный, вдоль кривой, эффекты для текста) | Л-4: Презентация и анимация графических и текстовых объектов. Средства организации чертежа (система координат, единицы измерения, слои, графические примитивы) | Л-5: Основные понятия о растровом и векторном изображении. Прикладное назначение программ для графического отображения физических процессов. Виды программного обеспечения для графики математического моделирования | Л-6: Виды графических программ векторной графики: Microsoft Visio, Corеl Draw, АutoCAD | Л-7: Окна программ векторной графики. Особенности импорта и экспорта изображений и макетов | Л-8: Панель инструментов программы. Библиотека элементов векторной графики | Л-9: Системы цветов в компьютерной графике: HSB, HSL, RGB, CMYK | Л-10: Методика рисования простых фигур и векторный способ формирования графических объектов | Л-11: Линии как объект векторной графики и их свойства | Л-12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | Л-13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | Л-14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | Л-15: Растровый способ формирования графических образов | Л-16: Вставка и редактирование рисунков. Геометрическое моделирование, преобразования растровых и векторных изображений | Л-17: Выделение и трансформация областей. Работа с текстом | Л-18: Тональная и цветовая коррекция и фильтры. Маски, каналы и ретушь | Л-19: Смешивание слоев, эффекты и стили слоев | Л-20: Виды систем графического моделирования: Mathсad, MatLab. Интерфейс пользователя систем Mathсad и MatLab | Л-21: Работа со встроенными функциями, массивами, векторами и матрицами | Л-22: Элементы графической визуализации. Графическая визуализация вычислений — построение графиков функций | Л-23: Основы работы с векторами и матрицами. Палитры математических знаков и документы Mathсad | |
|
|
| |
| |
| |
