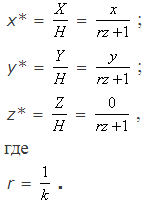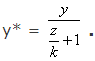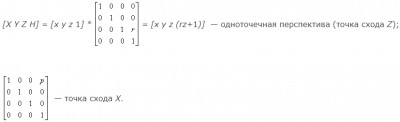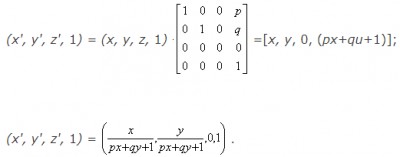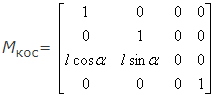ЭУМК Компьютерное моделирование
| Лекции: Введение | Л-1: Краткая история компьютерной графики. Основные понятия о машинной графике и основные задачи компьютерной графики. Классификация направлений и сферы применения компьютерной графики. Задачи курса | Л-2: Программное обеспечение для создания, просмотра и обработки графической информации | Л-3: Текстовый редактор. Работа с текстом (простой и фигурный, вдоль кривой, эффекты для текста) | Л-4: Презентация и анимация графических и текстовых объектов. Средства организации чертежа (система координат, единицы измерения, слои, графические примитивы) | Л-5: Основные понятия о растровом и векторном изображении. Прикладное назначение программ для графического отображения физических процессов. Виды программного обеспечения для графики математического моделирования | Л-6: Виды графических программ векторной графики: Microsoft Visio, Corеl Draw, АutoCAD | Л-7: Окна программ векторной графики. Особенности импорта и экспорта изображений и макетов | Л-8: Панель инструментов программы. Библиотека элементов векторной графики | Л-9: Системы цветов в компьютерной графике: HSB, HSL, RGB, CMYK | Л-10: Методика рисования простых фигур и векторный способ формирования графических объектов | Л-11: Линии как объект векторной графики и их свойства | Л-12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | Л-13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | Л-14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | Л-15: Растровый способ формирования графических образов | Л-16: Вставка и редактирование рисунков. Геометрическое моделирование, преобразования растровых и векторных изображений | Л-17: Выделение и трансформация областей. Работа с текстом | Л-18: Тональная и цветовая коррекция и фильтры. Маски, каналы и ретушь | Л-19: Смешивание слоев, эффекты и стили слоев | Л-20: Виды систем графического моделирования: Mathсad, MatLab. Интерфейс пользователя систем Mathсad и MatLab | Л-21: Работа со встроенными функциями, массивами, векторами и матрицами | Л-22: Элементы графической визуализации. Графическая визуализация вычислений — построение графиков функций | Л-23: Основы работы с векторами и матрицами. Палитры математических знаков и документы Mathсad | Дополнительные материалы: Практические работы Терминологический словарь Самостоятельные работы студента Методические рекомендации/указания Контрольные измерительные материалы Литература |
|
|
Лекция 13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике
|
|
| Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | | |
СодержаниеМатематическое описание плоских геометрических проекцийКаждую из проекций можно описать матрицей 4x4. Этот способ оказывается удобным, поскольку появляется возможность объединить матрицу проецирования с матрицей преобразования. Центральная (перспективная) проекция получается путем перспективного преобразования и проецирования на некоторую двухмерную плоскость «наблюдения». Перспективная проекция на плоскость Z=0 обеспечивается преобразованием
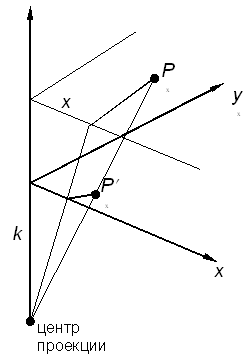
Рис. 13.14. Вычисление одноточечной перспективы или
Центр проекции находится в точке с координатами (0,0,-k) (рис.13.14), плоскость проецирования Z=0. Соотношения между x, y и x*, y* остаются теми же самыми. Рассматривая подобные треугольники, получим, что
аналогично
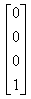
Координаты x*, y* являются преобразованными координатами. В перспективном проектировании преобразованное пространство не является евклидовым, так как ортогональность осей не сохраняется. При k=∞ получим аксонометрическое преобразование. Аффинное преобразование есть комбинация линейных преобразований, сопровождаемых переносом. Последний столбец в обобщенной матрице 4x4 должен быть равен
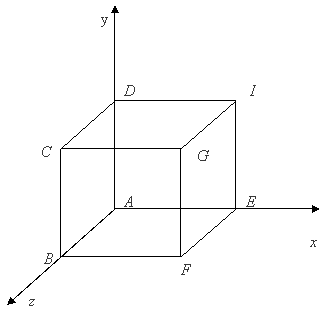
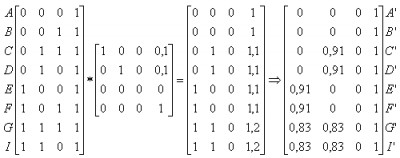
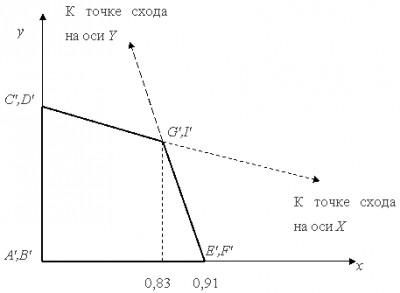
В этом случае H=1. Перспективному преобразованию может предшествовать произвольная последовательность аффинных преобразований. Таким образом, чтобы получить перспективные изображения из произвольной точки наблюдения вначале используют аффинные преобразования, позволяющие сформировать систему координат с осью Z вдоль желаемой линии визирования. Затем применяется перспективное преобразование. Аналогично перспективное преобразование, когда картинная плоскость перпендикулярна оси Z и совпадает с плоскостью Z=1/r. Центр проекции находится в центре координат: Двухточечная (угловая) перспектива. Для получения двухточечной перспективы в общей матрице преобразования устанавливают коэффициенты p и q: Такое преобразование приводит к двум точкам схода. Одна расположена на оси X в точке (1/p, 0, 0, 1), другая на оси Y в точке (0, 1/q, 0, 1). Рассмотрим это преобразование на получение проекции единичного куба (рис. 13.15.).
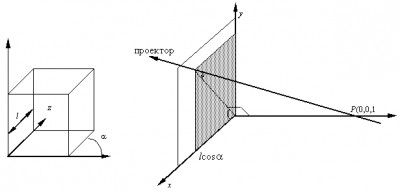
Рис. 13.15. Единичный куб для получения двухточечной проекции В результате получаем проекцию вида, представленного на рис. 13.16. Рис. 13.16. Двухточечная проекция единичного куба Для того чтобы создать диметрическую проекцию, необходимо выполнить следующее условие: sin2φ=sin2θ/(1- sin2θ). Одним способом выбора sinθ является сокращение оси Z в фиксированное число раз. При этом единичный вектор на оси Z, равный [0 0 1 1], преобразовывается к виду [X Y Z H] = [sinφ -cosφ×sinθ cosφ×cosθ 1] или x* = sinφ; y*= - cosφ sinθ. Таким образом, для диметрической проекции получаем φ = 20,705°: θ = 22,208°. Для образования изометрической проекции нужно в одинаковое число раз сократить все три оси. Для этого необходимо, чтобы выполнялось условие sin2φ=sin2θ/(1- sin2θ) и sin2φ=(1-2sin2θ)/(1- sin2θ). Таким образом, φ = 35,26439°; θ = 45°. Рассмотрим теперь косоугольную проекцию (рис. 13.17.), матрица может быть записана исходя из значений α и l. Проекцией точки P(0,0,1) является точка P′;(l cosa, l sinα, 0), принадлежащая плоскости xy. Направление проецирования совпадает с отрезком РР′, проходящим через две эти точки. Это направление есть Р′-Р = (l cosα, l sinα, -1). Направление проецирования составляет угол β с плоскостью xy. Теперь рассмотрим проекцию точки x, y, z и определим ее косоугольную проекцию (xp yp) на плоскости xy: xp=x+z(l cosα); yp=y+z(l sinα). Таким образом, матрица 4x4, которая выполняет эти действия и, следовательно, описывает косоугольную проекцию, имеет вид
Рис. 13.17. Вычисление косоугольных проекций Применение матрицы Мкос приводит к сдвигу и последующему проецированию объекта: плоскости с постоянной координатой z = z1 переносятся в направлении x на z1 l cosα и в направлении y на z1 l sinα и затем проецируется на плоскость z=0. Сдвиг сохраняет параллельность прямых, а также углы и расстояния в плоскостях, параллельных оси z. Для проекции Кавалье l=1, поэтому угол β=45°. Для проекции Кабине l=½, а β=arctg(2)=63,4°. В случае ортографической проекции l = 0 и β=90°, поэтому матрица ортографического проецирования является частным случаем косоугольной проекции. |
|
| Лекция 12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | |
| Лекция 13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | |
| Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | | |
| Лекция 14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | |