ЭУМК Компьютерное моделирование
| Лекции: Введение | Л-1: Краткая история компьютерной графики. Основные понятия о машинной графике и основные задачи компьютерной графики. Классификация направлений и сферы применения компьютерной графики. Задачи курса | Л-2: Программное обеспечение для создания, просмотра и обработки графической информации | Л-3: Текстовый редактор. Работа с текстом (простой и фигурный, вдоль кривой, эффекты для текста) | Л-4: Презентация и анимация графических и текстовых объектов. Средства организации чертежа (система координат, единицы измерения, слои, графические примитивы) | Л-5: Основные понятия о растровом и векторном изображении. Прикладное назначение программ для графического отображения физических процессов. Виды программного обеспечения для графики математического моделирования | Л-6: Виды графических программ векторной графики: Microsoft Visio, Corеl Draw, АutoCAD | Л-7: Окна программ векторной графики. Особенности импорта и экспорта изображений и макетов | Л-8: Панель инструментов программы. Библиотека элементов векторной графики | Л-9: Системы цветов в компьютерной графике: HSB, HSL, RGB, CMYK | Л-10: Методика рисования простых фигур и векторный способ формирования графических объектов | Л-11: Линии как объект векторной графики и их свойства | Л-12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | Л-13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | Л-14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | Л-15: Растровый способ формирования графических образов | Л-16: Вставка и редактирование рисунков. Геометрическое моделирование, преобразования растровых и векторных изображений | Л-17: Выделение и трансформация областей. Работа с текстом | Л-18: Тональная и цветовая коррекция и фильтры. Маски, каналы и ретушь | Л-19: Смешивание слоев, эффекты и стили слоев | Л-20: Виды систем графического моделирования: Mathсad, MatLab. Интерфейс пользователя систем Mathсad и MatLab | Л-21: Работа со встроенными функциями, массивами, векторами и матрицами | Л-22: Элементы графической визуализации. Графическая визуализация вычислений — построение графиков функций | Л-23: Основы работы с векторами и матрицами. Палитры математических знаков и документы Mathсad | Дополнительные материалы: Практические работы Терминологический словарь Самостоятельные работы студента Методические рекомендации/указания Контрольные измерительные материалы Литература |
|
|
Лекция 13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике
|
|
| Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | | |
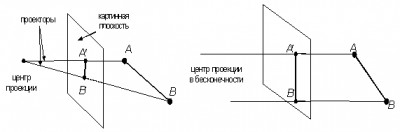
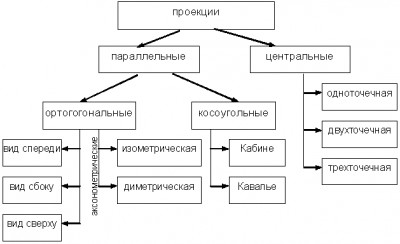
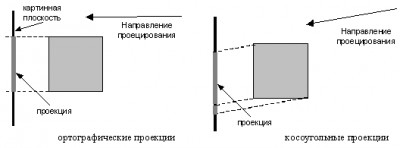
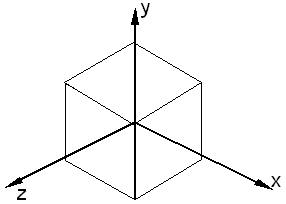
СодержаниеПроекцииВ общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в системы координат размерностью меньше чем n. Будем рассматривать случай проецирования трех измерений в два. Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, которые называются проекторами и которые проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию. Рис. 13.7. Центральная и параллельная проекции Определенный таким образом класс проекций существует под названием плоских геометрических проекций, так как проецирование производится на плоскость, а не на искривленную поверхность и в качестве проекторов используются прямые, а не кривые линии. Многие картографические проекции являются либо не плоскими, либо не геометрическими. Плоские геометрические проекции в дальнейшем будем называть просто проекциями. Проекции делятся на два основных класса (рис. 13.7): · параллельные (аксонометрические); · центральные (перспективные). Полная классификация проекций приведена на рис. 13.8. Рис. 13.8. Классификация проекций Параллельные проекции делятся на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости (рис. 13.9.): 1) ортографические – направления совпадают, т. е. направление проецирования является нормалью к проекционной плоскости; 2) косоугольные – направление проецирования и нормаль к проекционной плоскости не совпадают. Рис. 13.9. Ортографические и косоугольные проекции Наиболее широко используемыми видами ортографических проекций является вид спереди, вид сверху(план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям. Если проекционные плоскости не перпендикулярны главным координатным осям, то такие проекции называются аксонометрическими. При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояние можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами). Изометрическая проекция – нормаль к проекционной плоскости, (а следовательно и направление проецирования) составляет равные углы с каждой из главных координатных осей. Если нормаль к проекционной плоскости имеет координаты (a,b,c), то потребуем, чтобы |a| = |b| = |c|, или ±a=±b=±c, т. е. имеется 8 направлений (по одному в каждом из октантов), которые удовлетворяют этому условию. Однако существует лишь 4 различных изометрических проекции (если не рассматривать удаление скрытых линий), так как векторы (a, a, a) и (-a,-a,-a) определяют нормали к одной и той же проекционной плоскости. Изометрическая проекция (рис. 13.10.) обладает следующим свойством: все 3 главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом. Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом (120°).
Рис. 13.10. Изометрическая проекция единичного куба Косоугольные (наклонные) проекции сочетают в себе свойства ортографических проекций (видов спереди, сверху и сбоку) со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерить углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают. Двумя важными видами косоугольных проекций являются проекции: ·
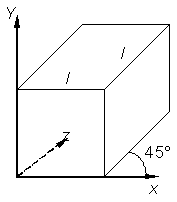
Рис. 13.11. Проекция Кавалье В проекции Кавалье (рис. 13.11.) направление проецирования составляет с плоскостью угол 45°. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т. е. укорачивание отсутствует.
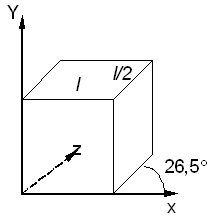
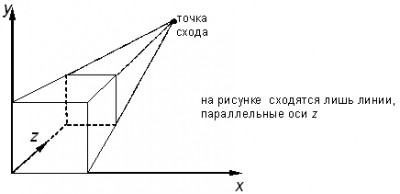
Рис. 13.12. Проекция Кабине Проекция Кабине (рис. 13.12.) имеет направление проецирования, которое составляет с проекционной плоскостью угол α = arctg(½) (≈26,5°). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют ½ их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом ½ больше согласуется с нашим визуальным опытом. Центральная проекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Точек схода бесконечно много. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно и от числа координатных осей, которые пересекают проекционную плоскость. 1. Одноточечная проекция (рис. 13.13). Рис. 13.13. Одноточечная перспектива 2. Двухточечная проекция широко применяется в архитектурном, инженерном и промышленном проектировании. 3. Трехточечные центральные проекции почти совсем не используются, во-первых, потому, что их трудно конструировать, а во-вторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией. |
|
| Лекция 12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | |
| Лекция 13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | |
| Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | | |
| Лекция 14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | |