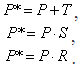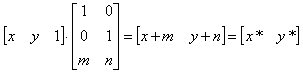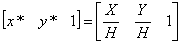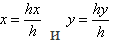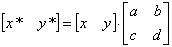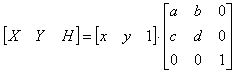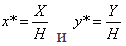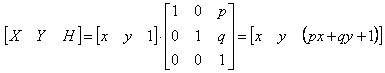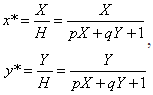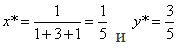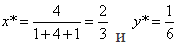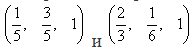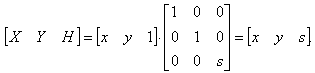ЭУМК Компьютерное моделирование
| Лекции: Введение | Л-1: Краткая история компьютерной графики. Основные понятия о машинной графике и основные задачи компьютерной графики. Классификация направлений и сферы применения компьютерной графики. Задачи курса | Л-2: Программное обеспечение для создания, просмотра и обработки графической информации | Л-3: Текстовый редактор. Работа с текстом (простой и фигурный, вдоль кривой, эффекты для текста) | Л-4: Презентация и анимация графических и текстовых объектов. Средства организации чертежа (система координат, единицы измерения, слои, графические примитивы) | Л-5: Основные понятия о растровом и векторном изображении. Прикладное назначение программ для графического отображения физических процессов. Виды программного обеспечения для графики математического моделирования | Л-6: Виды графических программ векторной графики: Microsoft Visio, Corеl Draw, АutoCAD | Л-7: Окна программ векторной графики. Особенности импорта и экспорта изображений и макетов | Л-8: Панель инструментов программы. Библиотека элементов векторной графики | Л-9: Системы цветов в компьютерной графике: HSB, HSL, RGB, CMYK | Л-10: Методика рисования простых фигур и векторный способ формирования графических объектов | Л-11: Линии как объект векторной графики и их свойства | Л-12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | Л-13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | Л-14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | Л-15: Растровый способ формирования графических образов | Л-16: Вставка и редактирование рисунков. Геометрическое моделирование, преобразования растровых и векторных изображений | Л-17: Выделение и трансформация областей. Работа с текстом | Л-18: Тональная и цветовая коррекция и фильтры. Маски, каналы и ретушь | Л-19: Смешивание слоев, эффекты и стили слоев | Л-20: Виды систем графического моделирования: Mathсad, MatLab. Интерфейс пользователя систем Mathсad и MatLab | Л-21: Работа со встроенными функциями, массивами, векторами и матрицами | Л-22: Элементы графической визуализации. Графическая визуализация вычислений — построение графиков функций | Л-23: Основы работы с векторами и матрицами. Палитры математических знаков и документы Mathсad | Дополнительные материалы: Практические работы Терминологический словарь Самостоятельные работы студента Методические рекомендации/указания Контрольные измерительные материалы Литература |
|
|
Лекция 13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике
|
|
| Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | | |
Содержание
Однородные координатыПреобразования переноса, масштабирования и поворота записываются в матричной форме в виде
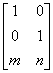
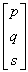
Очевидно, что перенос, в отличие от масштабирования и поворота, реализуется с помощью сложения. Это обусловлено тем, что вводить константы переноса внутрь структуры общей матрицы размером 2x2 не представляется возможным. Желательным является представление преобразований в единой форме – с помощью умножения матриц. Эту проблему можно решить за счет введения третьей компоненты в векторы точек [x y] и [x* y*], т. е. представляя их в виде [x y 1] и [x* y* 1] . Матрица преобразования после этого становится матрицей размером 3x2: Это необходимо, поскольку число столбцов в матрице, описывающей точку, должно равняться числу строк в матрице преобразования для выполнения операции умножения матриц. Таким образом,
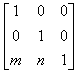
откуда следует, что константы m, n вызывают смещение х* и y* относительно х и у. Поскольку матрица 3x2 не является квадратной, она не имеет обратной матрицы. Эту трудность можно обойти, дополнив матрицу преобразования до квадратной размером 3x3. Например,
Заметим, что третья компонента векторов положения точек не изменяется при добавлении третьего столбца к матрице преобразования. Используя эту матрицу в соотношении, получаем преобразованный вектор [х* у* 1]. Добавление третьего элемента к вектору положения и третьего столбца к матрице преобразования позволяет выполнить смещение вектора положения. Третий элемент здесь можно рассматривать как дополнительную координату вектора положения. Итак, вектор положения [х у 1] при воздействии на него матрицы 3x3 становится вектором положения в общем случае вида [X Y Н]. Представленное преобразование было выполнено так, что [X Y Н] = [х* у* 1]. Преобразование, имеющее место в трехмерном пространстве, в нашем случае ограничено плоскостью, поскольку H = 1. Если, однако, третий столбец
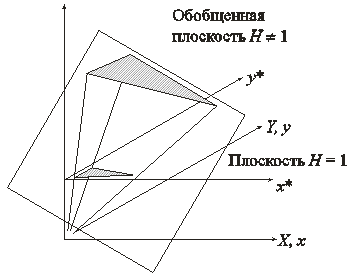
матрицы преобразования Т размера 3х3 отличен от 0, то в результате матричного преобразования получим [х у 1] =[Х Y Н], где Н ¹ 1. Плоскость, в которой теперь лежит преобразованный вектор положения, находится в трехмерном пространстве. Однако сейчас нас не интересует то, что происходит в трехмерном пространстве. Итак, найденные х* и у* получены с помощью пучка лучей, проходящих через начало координат. Результат преобразований показан на рис. 13.3.
Рис. 13.3. Геометрическое представление однородных координат Из рассмотрения подобных треугольников видно, что H/X=1/x* и H/Y=1/y*. Рассматривая три компоненты, запишем это в виде
Представление двумерного вектора трехмерным или в общем случае n-мерного вектора (п + 1)-мерным называют однородным координатным воспроизведением. При однородном координатном воспроизведении n-мерного вектора оно выполняется в (п + 1)-мерном пространстве, и конечные результаты в n-мерном пространстве получают с помощью обратного преобразования. Таким образом, двумерный вектор [х у] представляется трехкомпонентным вектором [hx hy h]. Разделив компоненты вектора на однородную координату h, получим
Не существует единственного однородного координатного представления точки в двумерном пространстве. Например, однородные координаты (12, 8, 4), (6, 4, 2) и (3, 2, 1) представляют исходную точку [3 2]. Для простоты вычислений выбираем [х у 1], чтобы представить непреобразованную точку в двумерных однородных координатах. Преобразование
в дополнительных координатах задается выражением в однородных координатах в виде
Выполнение указанных выше преобразований показывает, что Х = х*, Y = у*, а Н = 1. Равенство единице дополнительной координаты означает, что преобразованные однородные координаты равны исходным координатам. В общем случае Н ¹ 1, и преобразованные обычные координаты получаются за счет нормализации однородных координат, т. е.
Геометрически все преобразования х и у происходят в плоскости Н = 1 после нормализации преобразованных однородных координат. Преимущество введения однородных координат проявляется при использовании матрицы преобразований общего вида порядка 3x3
с помощью которой можно выполнять и другие преобразования, такие как смещение, операции изменения масштаба и сдвига, обусловленные матричными элементами а, b, с и d. Указанные операции рассмотрены ранее. Чтобы показать воздействие третьего столбца матрицы преобразований 3x3, рассмотрим следующую операцию:
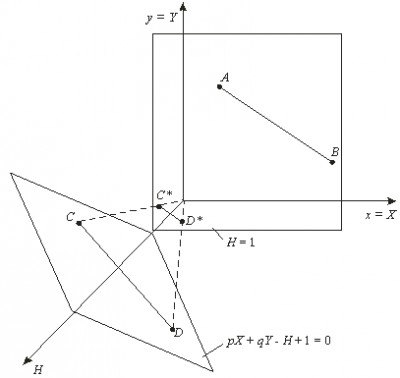
здесь Х = х, Y = у, а Н = рх + qy + 1. Переменная Н, которая определяет плоскость, содержащую преобразованные точки, представленные в однородных координатах, теперь образует уравнение плоскости в трехмерном пространстве. Это преобразование показано на рис. 13.4, где линия АВ, лежащая в плоскости ху, спроектирована на линию CD плоскости рХ + qY —Н + 1 = 0. Рис. 13.4. Преобразование линии в однородных координатах На рисунке величина р = q = 1.Выполним нормализацию для того, чтобы получить обычные координаты:
Полагая р = q = 1, для изображенных на рисунке точек А и В с координатами соответственно (1, 3) и (4, 1) получим
После преобразования А в С* и В в D* имеем
Однородные координаты для точек С* и D*, показанные на рисунке, соответственно равны
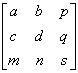
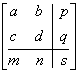
Результатом нормализации является перевод трехмерной линии CD в ее проекцию C*D* на плоскость Н = 1. Как показано на рисунке, центром проекции является начало координат. Основная матрица преобразования размером 3x3 для двумерных однородных координат может быть подразделена на четыре части:
Как мы видим, а, b, с и d осуществляют изменение масштаба, сдвиг и вращение; m и n выполняют смещение, а р и q — получение проекций. Оставшаяся часть матрицы, элемент s, производит полное изменение масштаба. Чтобы показать это, рассмотрим преобразование
Здесь Х = х, Y = у, а Н = s. Это дает х* = x/s и y* == y/s. В результате преобразования [х у 1] —> [x/s y/s 1] имеет место однородное изменение масштаба вектора положения. При s < 1 происходит увеличение, а при s > 1 — уменьшение масштаба. |
|
| Лекция 12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | |
| Лекция 13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | |
| Страницы: 1 | 2 | 3 | 4 | 5 | 6 | 7 | | |
| Лекция 14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | |