Объемы тел

Раздел 10. Интеграл и его применение

Тема 10.3 Геометрические приложения определенного интеграла

Площадь плоской области

Длина дуги кривой, заданной в явном виде

Длина дуги кривой, заданной в параметрическом виде

Длина дуги кривой, заданной в полярных координатах

Объемы тел

Страницы:  1  | 2 | 3 | 4 | 5 

Объемы тел

Рассмотрим задачу о нахождении объема тела, если известна зависимость площади его поперечного сечения  S(x)  плоскостью, перпендикулярной оси абсцисс. 
      Разобьем тело на тонкие слои. Каждый слой представляет собой цилиндр, объем которого равен  dV = S(x)dx, где  dx  – толщина слоя (высота цилиндра).

 
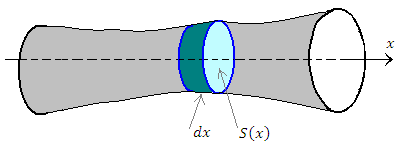
Рис. 1. Разбиение тела на тонкие слои параллельными друг другу плоскостями.

      Объем всего тела, заключенного в границах от  x = a  до  x = b, равен сумме объемов образующих его элементов:

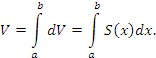(1)

      Если тело образовано вращением дуги кривой  y = f(x) 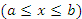  вокруг оси  0x, то площадь  S(x)  поперечного сечения тела плоскостью, перпендикулярной оси абсцисс, представляет собой круг радиуса  y = f(x). Тогда  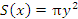и, следовательно,

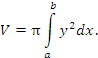(2)

***

Пример 2.  Найти объем параболоида вращения  . Решение. Такой параболоид может быть получен вращением дуги параболы    вокруг оси  0x. Следовательно,

Страницы:  1  | 2 | 3 | 4 | 5