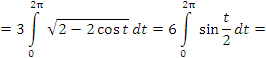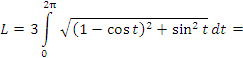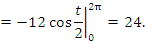Длина дуги кривой, заданной в параметрическом виде

Раздел 10. Интеграл и его применение

Тема 10.3 Геометрические приложения определенного интеграла

Площадь плоской области

Длина дуги кривой, заданной в явном виде

Длина дуги кривой, заданной в параметрическом виде

Длина дуги кривой, заданной в полярных координатах

Объемы тел

Страницы:  1  | 2 | 3 | 4 | 5 

Длина дуги кривой, заданной в параметрическом виде

 Пусть пространственная кривая задана уравнениями в параметрической форме:

(1)

      Длина пространственного отрезка описывается формулой

(2)

      Преобразуем это выражение, умножив и поделив его на  dt:

(3)

      Затем разделим каждое слагаемое в числителе на знаменатель и представим результат в виде

(4)

где  x',  y' и  z' – производные функций  x(t),  y(t)  и  z(t)  по переменной  t. 
      Тогда

(5)

      Полученная формула включает в себя формулу

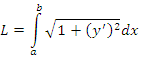(6)

в качестве частного случая. Действительно, если кривая лежит в плоскости  x0y, то рассматривая переменную  x  в качестве параметра  t, мы имеем  x = x,  y = y(x)  и  z = 0. Тогда формула (5) влечет за собой формулу (6).

Пример 1.  Найти длину одной арки циклоиды

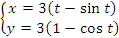
Решение. Заметим, что параметр  t принимает на концах первой арки циклоиды значения 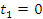 и .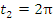
Учитывая, что 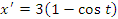   и 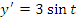 , получаем

Страницы:  1  | 2 | 3 | 4 | 5