Раздел 10. Интеграл и его применение
Тема 10.3 Геометрические приложения определенного интеграла
 Площадь плоской области Площадь плоской области |
 Длина дуги кривой, заданной в явном виде Длина дуги кривой, заданной в явном виде |
 Длина дуги кривой, заданной в параметрическом виде Длина дуги кривой, заданной в параметрическом виде |
 Длина дуги кривой, заданной в полярных координатах Длина дуги кривой, заданной в полярных координатах |
 Объемы тел Объемы тел |

Площадь плоской области
- Пусть границы области заданы уравнениями линий в декартовой системе координат. Тогда для нахождения площади этой области нужно:
- разбить фигуру на бесконечно малые прямоугольники, стороны которых параллельны координатным осям;
- записать формулу для площади такого прямоугольника;
- проинтегрировать полученное выражение по соответствующему промежутку.
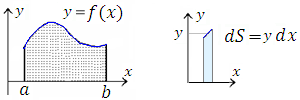
-
Рис. 1. Площадь области, ограниченной кривой y = f(x) и осью 0x от x = a до x = b.
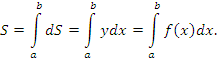

-
Рис. 2. Площадь области, ограниченной линиями y = f(x) и y = g(x) от x = a до x = b.

- Если линия, ограничивающая область, задана уравнениями в параметрической форме,
то площадь этой области описывается формулой ,
,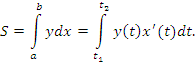
- Пусть область ограниченна графиком функции
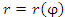 , заданной в полярной системе координат, и лучами
, заданной в полярной системе координат, и лучами 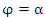 и
и 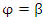 .
.
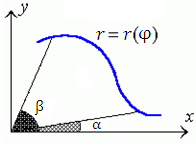
-
Рис. 3. Область, ограниченная кривой
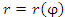 и лучами
и лучами 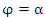 и
и 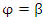 .
.
Такую фигуру можно разбить на бесконечное число элементов, представляющих собой круговые секторы (см. рисунок 4).
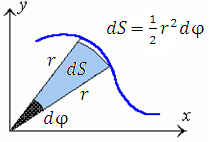
Рис. 4. Элемент разбиения фигуры, границы которой описываются ура
Площадь кругового сектора равна половине произведения сторон на угол (выраженный в радианной мере) между ними. Стороны бесконечно узкого сектора совпадают друг с другом и равны расстоянию r от соответствующей точки кривой до начала координат. Следовательно,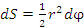 и
и
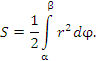
Примеры:
Пример 1. Найти площадь области, заключенной между линиями y = 3x и 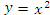 . .Решение. Абсциссы точек пересечения заданных линий являются пределами интегрирования и представляют собой решения уравнения 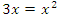 : :
x1 = 0, и x2 = 3. Тогда 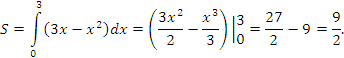 |
***
Пример 2. Найти площадь фигуры, ограниченной графиком функции 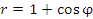 . .
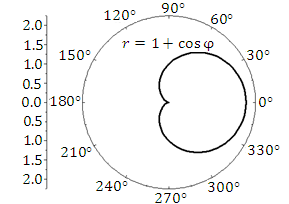 Рис. 1. Деления на окружности соответствуют значениям полярной координаты 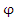 . Деления на вертикальной линии – значениям полярной координаты r. . Деления на вертикальной линии – значениям полярной координаты r.Решение. 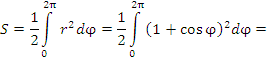 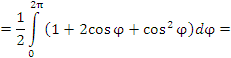 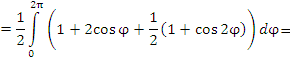 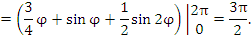 |
***
Пример 3. Найти площадь фигуры, ограниченной осью 0x и одной аркой циклоиды
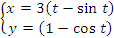 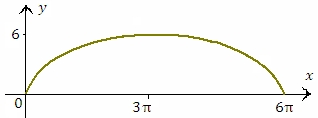  . .Рис. 2. Первая арка циклоиды. Циклоида представляет собой линию, которую описывает точка на ободе катящегося без проскальзывания колеса. Решение. Представим интеграл 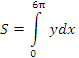 в терминах переменной t. в терминах переменной t.Учитывая, что x(0)=0, 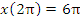 и и 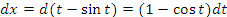 , получаем , получаем
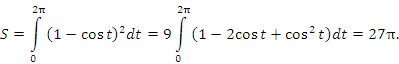 |
***
Пример 4. Найти площадь круга радиуса R.
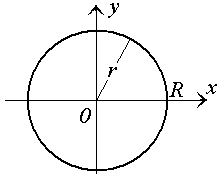 . .Рис. 3. Окружность радиуса R Решение. Уравнение окружности 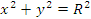 принимает наиболее простой вид при переходе к полярной системе координат: r = R. принимает наиболее простой вид при переходе к полярной системе координат: r = R.Тогда 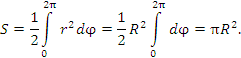 |
***
Пример 5. Найти площадь эллипса с полуосями a и b.
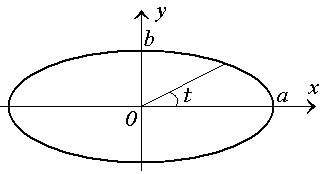 Рис. 4. Эллипс с полуосями a и b. Решение. Представим уравнение эллипса в параметрическом виде: 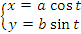 Найдем пределы интегрирования: x = – a при 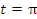 ; ;x = a при t = 0. Учитывая, что dx = 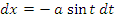 и меняя местами пределы интегрирования, вычисляем площадь: и меняя местами пределы интегрирования, вычисляем площадь:
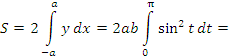 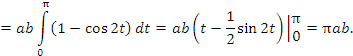 |
***
Пример 6. Вычислить площадь фигуры, заключенной между параболой 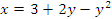 и осью ординат. и осью ординат.
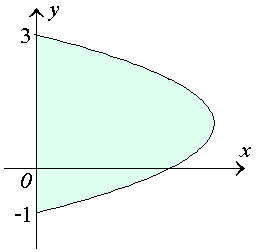 Рис. 5. Область, ограниченная параболой 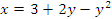 и осью ординат. и осью ординат.Решение. Поскольку переменные x и y поменялись ролями, то площадь вычисляется по формуле 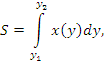 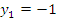 и и 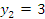 – точки пересечения параболы с осью ординат. – точки пересечения параболы с осью ординат.Таким образом, 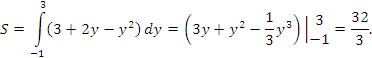 |