Длина дуги кривой, заданной в полярных координатах

Раздел 10. Интеграл и его применение

Тема 10.3 Геометрические приложения определенного интеграла

Площадь плоской области

Длина дуги кривой, заданной в явном виде

Длина дуги кривой, заданной в параметрическом виде

Длина дуги кривой, заданной в полярных координатах

Объемы тел

Страницы:  1  | 2 | 3 | 4 | 5 

Длина дуги кривой, заданной в полярных координатах

Пусть кривая лежит в плоскости  x0y  и описывается уравнением  r = r(φ)  в полярных координатах. Представим выражение 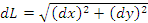 в виде

.

(1)

      Выразим декартовые координаты  x  и  y  через полярные координаты  r  и  φ:

      Продифференцируем эти выражения по переменной  φ:

      Нетрудно показать, что

(4)

      Следовательно,

(5)

Пример 1.  Найти длину первого витка спирали Архимеда  r = φ.

Решение. Концам первого витка соответствуют значения 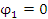   и 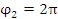   полярного угла  φ. Тогда

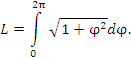
Интегрируем по частям, положив 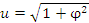   и 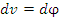 , что влечет

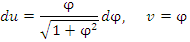
и

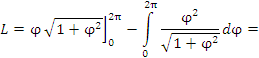
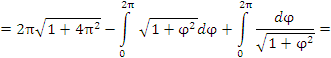
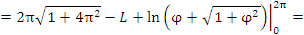
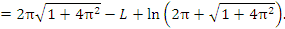
Таким образом,

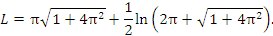
Страницы:  1  | 2 | 3 | 4 | 5