Бесконечно большие последовательности

Раздел 9. Начала математического анализа

Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции

Пределы числовых последовательностей

Понятие числовой последовательности

Ограниченные последовательности

Бесконечно малые последовательности

Свойства бесконечно малых последовательностей

Предел последовательности

Свойства пределов последовательностей

Бесконечно большие последовательности

Теоремы о монотонных последовательностях

Число e

Страницы: 1 | 2 | 3

Бесконечно большие последовательности

Последовательность 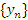   называется бесконечно большой (б/б), если абсолютные величины всех ее элементов – начиная с некоторого номера  N  – превышают любое сколь угодно большое наперед заданное число  E > 0. Другими словами,  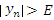   при  n > N. 
      Легко показать, что общий член 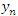   бесконечно большой последовательности может быть представлен в виде

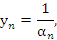
где 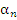   –некоторая бесконечно малая последовательность. 

      Чтобы наглядно представить себе смысл термина “бесконечно большая величина”, поделите число 1 на 0.1, затем на 0.01, 0.001, 0.000001 и так далее. 

      Понятие бесконечно большой последовательности можно также сформулировать в терминах  E-окрестности бесконечно удаленной точки. 
      Говорят, что элементы содержатся в  E-окрестности бесконечно удаленной точки, если их абсолютные величины превосходят число  E. Другими словами, под  E-окрестностью бесконечно удаленной точки понимается один из интервалов 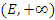 или 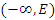, либо оба эти интервалы. Можно также сказать, что последовательность является бесконечно большой, если все ее элементы, начиная с некоторого номера, попадают в  E-окрестность бесконечно удаленной точки. 
      Для обозначения бесконечно больших последовательностей используются символические выражения вида

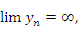
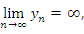
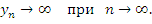
При этом говорят, что последовательность 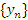   имеет бесконечный предел или что переменная  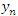  стремится к бесконечности. 
      Очевидно, что любая бесконечно большая последовательность является неограниченной и расходящейся. 

      Типичные особенности поведения бесконечно больших величин при 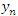   показаны на рисунке 14.

 
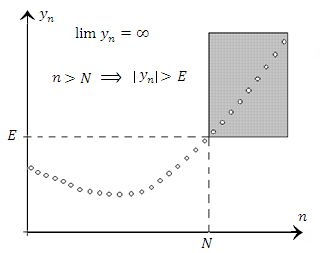
Рис. 14. Пример расходящейся последовательности  .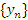

      Утверждение, что последовательность 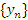   является бесконечно большой, а ее элементы сохраняют знак “+” (по крайней мере для достаточно больших номеров), записывается в виде  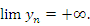  и иллюстрируется рисунком 15.

 
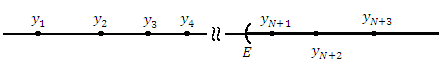
Рис. 15. Последовательность 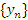 , элементы которой стремятся к  + ∞  при  .

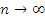      Аналогичным образом интерпретируется выражение вида  .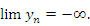

 
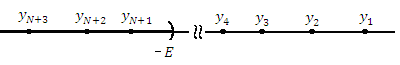
Рис. 16. Бесконечно большая последовательность, элементы которой сохраняют знак “–” для достаточно больших номеров  n.

 Примеры бесконечно больших последовательностей:

1. Последовательность    является бесконечно большой и имеет своим пределом  + ∞.


2. Последовательность    является бесконечно большой, поскольку

   
   
   Рис. 17. Бесконечно большая последовательность.

   
   Эти интуитивные соображения можно сопроводить формальным доказательством. Фактически достаточно показать, что неравенство

   

   выполняется для любого сколь угодно большого числа  E > 0, начиная с некоторого номера  N.
   Очевидно, что

   

   Выберем в качестве номера  N  любое целое число, удовлетворяющее условию  . Тогда неравенство

   

   влечет за собой неравенство    и, следовательно,

   

Теоремы о монотонных последовательностях

Теорема 3. Всякая ограниченная сверху монотонно возрастающая последовательность имеет конечный предел. 

Доказательство. Пусть  A  – наименьшая верхняя граница последовательности 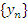 . Это означает, что

	•	все члены этой последовательности удовлетворяют неравенству  ;
	•	для любого произвольно малого числа  ε > 0  разность  A – ε  не является верхней границей последовательности.

Следовательно, существует элемент 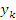 , превосходящий число  A – ε:

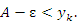
Поскольку последовательность 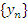   является монотонно возрастающей, то

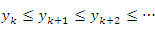
Таким образом, все члены последовательности 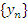 , начиная с  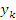, удовлетворяют неравенству

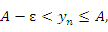
что влечет за собой утверждение

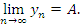
Теорема 4. Всякая ограниченная снизу монотонно убывающая последовательность имеет конечный предел. 

Число e

Теорема. Последовательность с общим членом 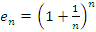   имеет конечный предел при  . 

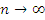Замечание. Для обозначения этого предела используется символ e:

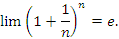
Число  e  является иррациональным, приближенное значение которого равно

e = 2.71828182845904523536028747135266249775724709…

Доказательство. Покажем сначала, что 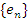   представляет собой монотонно возрастающую последовательность. Согласно биному Ньютона,

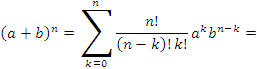
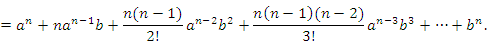
Полагая 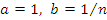 , получим

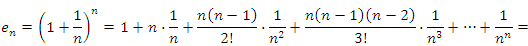
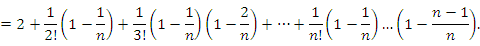
Аналогично,

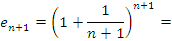
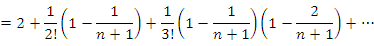
Сравним выражения для 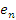   и  .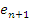 
Во-первых, оба эти выражения содержат только положительные слагаемые. 
Во-вторых, начиная со второго слагаемого, каждый член в выражении для 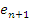   превышает соответствующий член выражения для  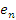, поскольку

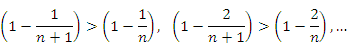
В-третьих, выражение для 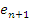   состоит из большего числа слагаемых. Следовательно,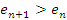   

Далее докажем, что последовательность 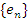   является ограниченной. Действительно, первый член любой монотонно возрастающей последовательности является ее наибольшей нижней границей и, таким образом,  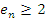  для всех натуральных значений  n. 

Перейдем к доказательству существования верхней границы. Очевидно, что

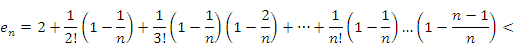
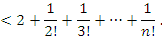
Кроме того, 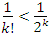   для всех  k > 3. Тогда

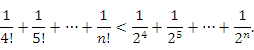
Правая часть этого неравенства представляет собой сумму членов убывающей геометрической прогрессии. В качестве верхней границы этой суммы выступает любое число 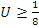 . Таким образом, последовательность с общим членом

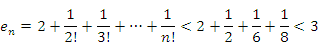
представляет собой ограниченную монотонно возрастающую последовательность и, следовательно, имеет конечный предел – согласно теореме о монотонных последовательностях.

Страницы: 1 | 2 | 3