Раздел 9. Начала математического анализа
Тема 9.1 Последовательности Числовые последовательности и их свойства. Предел числовой последовательности. Предел функции
Пределы числовых последовательностей
Понятие числовой последовательности
Математическое понятие числовой последовательности находится в полном соответствии с нашим интуитивным представлением о последовательности событий, что подразумевает их конкретный порядок. Говоря о числовой последовательности, мы имеем в виду множество значений функции натурального аргумента. Для обозначения последовательностей используются выражения вида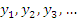 
или 
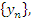где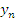 
– общий член последовательности, определяющий все ее элементы.
Последовательность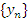 
называется монотонно возрастающей, если каждый ее последующий член больше предыдущего: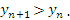 
Последовательность 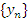называется монотонно убывающей, если каждый ее последующий член меньше предыдущего: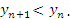 
Элементам числовой последовательности можно поставить в соответствие точки числовой оси:
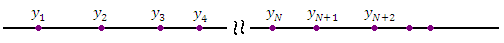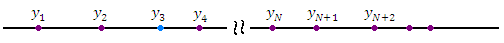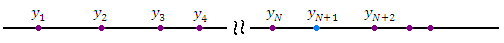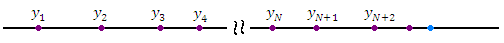
Существуют и другие способы графического представления элементов последовательности, например, в виде графика функции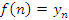 
:
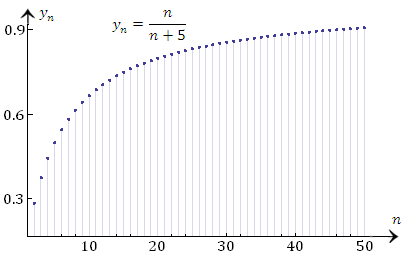
Рис. 1. Графическая иллюстрация монотонно возрастающей последовательности.
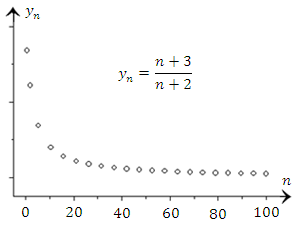
Рис. 2. Монотонно убывающая последовательность.
Примеры последовательностей:
- Элементы арифметической прогрессии
образуют последовательность с общим членом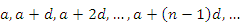
:
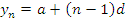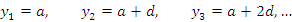
- Элементы геометрической прогрессии
образуют последовательность с общим членом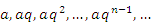
:
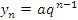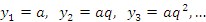
- Пусть
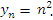Тогда, в частности,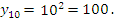 
- Элементами последовательности не обязательно должны быть различные числа. Так, если yn = 1, то последовательность имеет вид
1, 1, ..., 1, ...
- Общий член
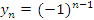определяет последовательность вида
1, –1, 1, –1, ...
- Общий член
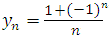задает последовательность
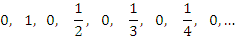
- Последовательность
1, 0, –1, 0, 1, 0, –1, 0, ...
описывается общим членом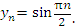
- Рассмотрим сумму первых n элементов последовательности
:
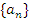Тогда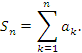
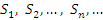представляет собой последовательность частичных сумм.
Примеры монотонных последовательностей:
- Последовательность
с общим членом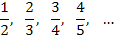
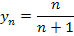является монотонно возрастающей. - Последовательность
с общим членом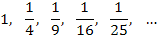
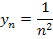является монотонно убывающей.
Примеры немонотонных последовательностей:
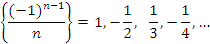
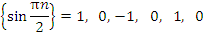
Ограниченные последовательности
Последовательность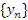 
называется ограниченной сверху, если существует такое число U, что 
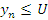для любых номеров n. При этом число U называется верхней границей последовательности.
Последовательность 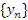называется ограниченной снизу, если существует такое число L, что 
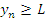для любых номеров n. Число L называется нижней границей последовательности.
Последовательность 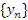называется ограниченной, если существуют такие числа L и U, что 
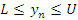для всех n = 1,2,3,…
Теорема 1. Любая ограниченная сверху последовательность имеет наименьшую верхнюю границу.
Теорема 2. Любая ограниченная снизу последовательность имеет наибольшую нижнюю границу.
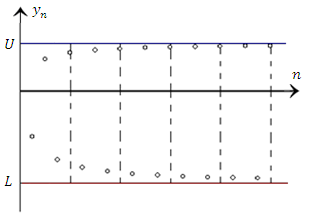
Рис. 3. Наименьшая верхняя и наибольшая нижняя границы последовательности показаны горизонтальными линиями, расположенными вверху и внизу соответственно.
|
Примеры ограниченных последовательностей:
|
для всех 
Бесконечно малые последовательности
Последовательность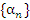 
называется бесконечно малой (б/м), если значения всех ее элементов – начиная с некоторого номера – становятся по абсолютной величине меньшими любого положительного числа ε.
Можно сказать и иначе: последовательность 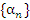является бесконечно малой, если для любого положительного числа ε существует лишь конечное число ее членов, превосходящих ε. В символической форме это утверждение записывается в виде
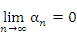
или
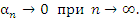
Если элементы последовательности изображать точками числовой оси, то члены бесконечно малой последовательности с ростом номера n приближаются неограниченно близко к точке 0, которая является точкой сгущения (или предельной точкой) бесконечно малой последовательности при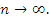 
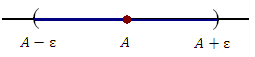
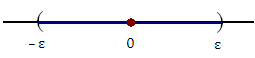
Отметим, что открытый интервал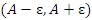 
с центром в точке A называется ε-окрестностью точки A. В частности, ε-окрестность нуля представляет собой открытый интервал (-ε,ε).
 |
 |
|
| Рис. 4. ε-окрестность точки A. | Рис. 5. ε-окрестность нуля. |
Любая ε-окрестность нуля содержит все точки бесконечно малой последовательности 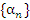, начиная с некоторого номера.
Рис. 6. Вне ε-окрестности нуля может находиться лишь конечное число точек бесконечно малой последовательности.
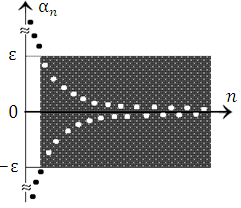
Рис. 7. Осциллирующая бесконечно малая последовательность.
Свойства бесконечно малых последовательностей
Свойство 1. Произведение бесконечно малой последовательности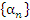 
и ограниченной последовательности 
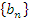есть бесконечно малая последовательность 
.
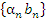Доказательство. Ограниченность последовательности 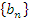означает, что 
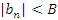для всех 
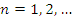, где B – некоторое положительное число. Выберем сколь угодно малое число ε > 0. Согласно определению бесконечно малой последовательности существует такой номер N, начиная с которого величины 
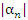становятся меньше любого положительного числа и, в частности, 
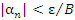. Тогда
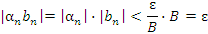
для всех n > N, что доказывает утверждение.
Следствие. Умножение бесконечно малой последовательности на любое число дает бесконечно малую последовательность.
Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая.
Доказательство. Рассмотрим сначала сумму двух бесконечно малых величин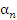 
и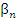 
.
Пусть ε – произвольное положительное число. Тогда существуют номер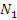 
, начиная с которого бесконечно малые величины 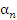становятся меньше числа 
:
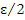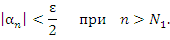
Аналогично,
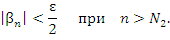
Обозначим символом N наибольший из номеров 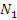и 
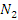. Тогда для всех номеров n > N выполняется неравенство
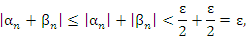
выражающее справедливость доказываемого утверждения.
Переходя к случаю суммы произвольного конечного числа бесконечно малых величин, заметим, что любая пара бесконечно малых в этой сумме может быть представлена одной бесконечно малой. Затем каждая пара полученных бесконечно малых может быть заменена одной бесконечно малой и так далее, что в конечном итоге позволит свести рассматриваемую сумму к единственной бесконечно малой.
Примеры бесконечно малых последовательностей
|
1. Последовательность с общим членом |
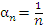является бесконечно малой, поскольку все ее члены, начиная с некоторого номера, становятся меньше любого положительного числа ε.
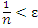эквивалентно неравенству 
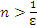и, следовательно, выполняется для всех 
одновременно, если в качестве номера N выбрать любое целое число, которое больше, чем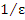 
. Полагая, например, ε = 0.001, получаем, что 
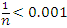для всех n > 1000.2. Последовательность 
является бесконечно малой при 
. Действительно, каждый член этой последовательности меньше соответствующего члена бесконечно малой последовательности 
и, следовательно, элементы 
образуют бесконечно малую последовательность:
Рис. 8. Бесконечно малая последовательность .
Переменная  является бесконечно малой при , поскольку для любого сколь угодно малого числа ε > 0 неравенство  выполняется для всех номеров 
|
.
при 
при 
при 
при 
при 
при 
при 
.
, получим, что условие 
влечет за собой неравенство
.
Учитывая, что 
выберем
