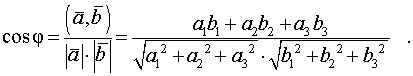Понятие вектора Понятие вектора |
 Координаты вектора Координаты вектора |
 Длина вектора Длина вектора |
 Равенство векторов Равенство векторов |
 Умножение вектора на число Умножение вектора на число |
 Сложение и вычитание векторов Сложение и вычитание векторов |
 Скалярное произведение векторов Скалярное произведение векторов |
 Примеры решения задач Примеры решения задач |
![]()
Понятие вектора
Рассмотрим две произвольные точки. Если соединить эти точки стрелкой (рис.1),

Рис.1
то мы получим вектор.
Точку, из которой стрелка выходит, называют началом вектора. Точку, в которую стрелка входит, называют концом вектора.
Чтобы отличить вектор от отрезка с концами в тех же точках, используют обозначение ![]() (рис.2) или
(рис.2) или ![]() (рис.3).
(рис.3).
 |
 |
| Рис.2 | Рис.3 |
Иногда для вектора используют обозначения ![]() (рис.4) или
(рис.4) или ![]() (рис.5).
(рис.5).
 |
 |
| Рис.4 | Рис.5 |
Если две точки (начало и конец вектора) совпадают, то говорят, что эти точки задают нулевой вектор.
Координаты вектора
Рассмотрим произвольный вектор ![]() и предположим, что в пространстве задана декартова прямоугольная система координат Oxyz (рис.6).
и предположим, что в пространстве задана декартова прямоугольная система координат Oxyz (рис.6).
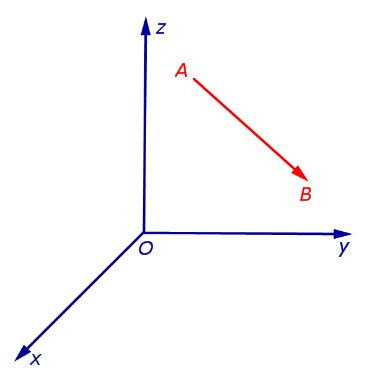
Рис.6
Если в системе координат Oxyz точки A и B имеют координаты
| A = (a1; a2; a3) и B = (b1; b2; b3) , | (1) |
то координатами вектора ![]() называют набор чисел
называют набор чисел
|
|
(2) |
Этот определение часто формулируют так: «Для того, чтобы найти координаты вектора, нужно из координат конца вектора вычесть координаты начала вектора».
Замечание. В случае, когда рассматриваются векторы, лежащие на некоторой координатной плоскости, в формулах (1) и (2) не будет третьих координат. Если же рассматриваются векторы, лежащие на некоторой координатной прямой, то в формулах (1) и (2) останутся только первые координаты.
Длина вектора
Длиной (модулем) произвольного вектора ![]() называют длину отрезка AB
называют длину отрезка AB
Длина вектора ![]() , координаты которого имеют вид
, координаты которого имеют вид
![]()
вычисляется по формуле
| (3) |
Этот факт часто формулируют так: «Длина вектора равна корню квадратному из суммы квадратов его координат».
Замечание. В случае, когда рассматриваются векторы, лежащие на координатной плоскости, формула (3) принимает вид
| (4) |
и совпадает с формулой, позволяющей найти расстояние между двумя точками координатной плоскости.
В случае, когда рассматриваются векторы, лежащие на координатной прямой, формулы (3) и (4) принимают вид
![]() .
.
Равенство векторов
Векторы называют коллинеарными векторами, если они лежат на одной прямой или на параллельных прямых.
Два вектора
![]() и
и ![]()
являются коллинеарными векторами тогда и только тогда, когда их координаты пропорциональны.
Другими словами, векторы являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства
a1 = tb1, a2 = tb2, a3 = tb3.
Два вектора называют сонаправленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 7.
Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в одну сторону (концы векторов будут лежать на одном луче).
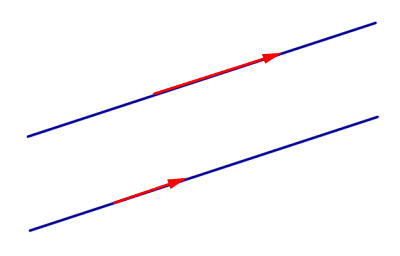
Рис.7
Два вектора называют противоположно направленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 8.
Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в разные стороны (концы векторов будут лежать по разные стороны от их общего начала).
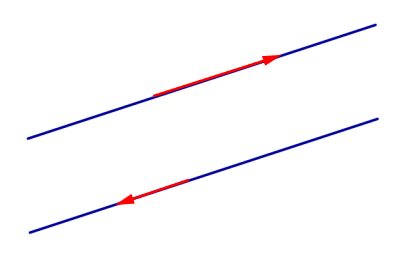
Рис.8
Определение. Два вектора равны, если, во-первых, они сонаправленные, а, во-вторых, имеют одинаковую длину.
Другими словами, если совместить начала этих векторов, то их концы совпадут.
Замечание. Два вектора равны тогда и только тогда, когда у них совпадают наборы координат.
Умножение вектора на число
В результате умножения любого вектора ![]() на любое действительное число k получается такой вектор
на любое действительное число k получается такой вектор ![]() , который удовлетворяет следующим условиям:
, который удовлетворяет следующим условиям:
- При k > 0 вектор
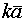 сонаправлен с вектором
сонаправлен с вектором 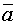 ;
; - При k < 0 вектор
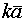 противоположно направлен с вектором
противоположно направлен с вектором 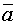 ;
; - Длина вектора
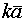 равна длине вектора
равна длине вектора 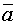 , умноженной на число |k|.
, умноженной на число |k|.
Если вектор ![]() имеет координаты
имеет координаты
![]()
то вектор ![]() имеет координаты
имеет координаты
![]()
Другими словами, если вектор умножается на число, то и все его координаты умножаются на это число.
Сложение и вычитание векторов
Для того, чтобы найти сумму двух произвольных векторов ![]() и
и ![]() нужно совместить начало вектора
нужно совместить начало вектора ![]() с концом вектора
с концом вектора ![]() . Тогда началом вектора
. Тогда началом вектора ![]() будет начало вектора
будет начало вектора ![]() , а концом вектора
, а концом вектора ![]() будет конец вектора
будет конец вектора ![]() (рис.9).
(рис.9).
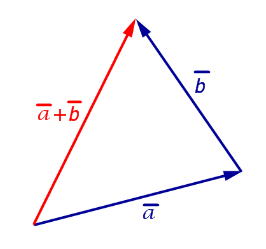
Рис.9
При этом, если
![]() и
и ![]()
то
![]()
Этот факт часто формулируют так: «При сложении векторов их координаты складываются».
Для того, чтобы найти разность двух произвольных векторов ![]() и
и ![]() нужно воспользоваться формулой
нужно воспользоваться формулой
![]()
Операция вычитания двух векторов наглядно изображена на рисунке 10.
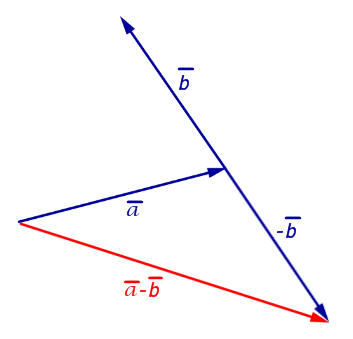
Рис.10
При этом, если
![]() и
и ![]()
то
![]()
Этот факт часто формулируют так: «Для того, чтобы найти координаты вектора ![]() , нужно из координат вектора
, нужно из координат вектора ![]() вычесть координаты вектора
вычесть координаты вектора ![]() ».
».
Скалярное произведение векторов
Определение. Скалярным произведением векторов ![]() и
и ![]() , которое обозначается
, которое обозначается ![]() называют число, равное произведению длин векторов
называют число, равное произведению длин векторов ![]() и
и ![]() , умноженному на косинус угла между этими векторами (рис.11).
, умноженному на косинус угла между этими векторами (рис.11).
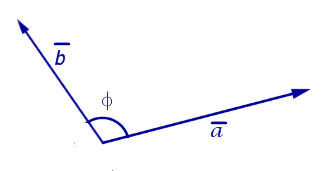
Рис.11
Таким образом,
| (5) |
Из формулы (5) вытекает соотношение
![]()
которое можно сформулировать так: «Модуль вектора равен корню квадратному из скалярного произведения вектора на себя».
Следствие 1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Утверждение. Если в декартовой прямоугольной системе координат векторы имеют координаты
| (6) |
то их скалярное произведение выражается формулой:
| (7) |
Другими словами, в декартовой прямоугольной системе координат скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Замечание. Зная координаты векторов (6), из формул (3), (5) и (7) можно найти косинус угла между векторами ![]() и
и ![]()
|
|
(8) |
Примеры решения задач
Пример 1. При каких значениях параметра p векторы ![]() и
и ![]() перпендикулярны?
перпендикулярны?
Решение. Воспользовавшись формулой (7), получим
![]()
Ответ: 4.
Пример 2. При каких значениях параметров α и β векторы (α; – 2; 5) и (1; β; – 4) коллинеарны?
Решение. Векторы, в силу изложенного выше, являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства:
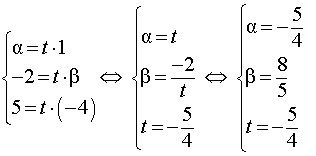
Ответ: ![]() .
.
Пример 3. Длины векторов ![]() и
и ![]() равны 2 и 1 , соответственно, а угол между ними равен 60° . Найти длину вектора
равны 2 и 1 , соответственно, а угол между ними равен 60° . Найти длину вектора ![]() .
.
Решение. Рассмотрим рисунок 12.
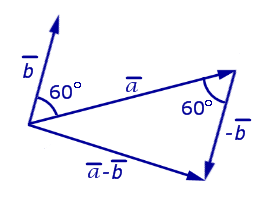
Рис.12
Воспользовавшись теоремой косинусов, получим
![]()
Ответ: ![]() .
.
Пример 4. Длины векторов ![]() и
и ![]() равны 3 и 1, соответственно, а угол между ними равен 60°. Найти длину вектора
равны 3 и 1, соответственно, а угол между ними равен 60°. Найти длину вектора ![]() .
.
Решение. Рассмотрим рисунок 13.
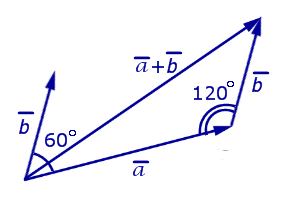
Рис.13
Воспользовавшись теоремой косинусов, получим
![]()
Ответ: ![]() .
.
Пример 5. Найти угол между векторами (3; 6; 2) и (4; 7; 4) .
Решение. Воспользовавшись формулой (8), получим
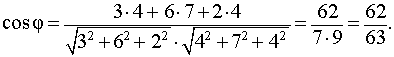
Ответ: 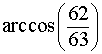 .
.