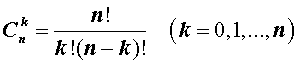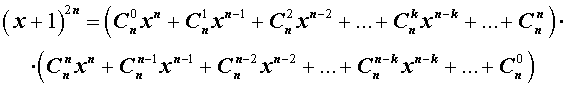 Формула бинома Ньютона |
| Связь бинома Ньютона с треугольником Паскаля |
| Свойства биномиальных коэффициентов |
Формула бинома Ньютона
В таблице 1 приведены формулы для натуральных степеней бинома
(x + y)n
в случаях, когда n = 1, 2, 3, 4, 5, 6.
Таблица 1. – Степень суммы
| Название формулы | Формула |
| Квадрат (вторая степень) суммы |
(x + y)2 = x2 + 2xy + y2 |
| Куб (третья степень) суммы | (x + y)3 = x3 + 3x2y + 3xy2 + y3 |
| Четвертая степень суммы | (x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4 |
| Пятая степень суммы | (x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| Шестая степень суммы | (x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
| … | … |
Утверждение. Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона:
|
|
(1) |
где
|
|
(2) |
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона, а числа сочетаний 
– коэффициентами разложения или биномиальными коэффициентами.
Если в формуле (1) заменить y на – y , то мы получим формулу для n - ой степени разности:
Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
| № | Треугольник Паскаля |
| 0 |  |
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 6 |  |
| … | … |
Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
| 1 |  |
| 2 |
|
| 3 |
|
| 4 |
|
к доказательству которых мы сейчас и переходим.
Докажем сначала равенство 1.
Это равенство отражает основное свойство треугольника Паскаля, заключающееся в том, что в каждой из строк треугольника Паскаля, начиная со строки с номером 2 , между числами 1 стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.
Для доказательства равенства 1 воспользуемся формулой (2):
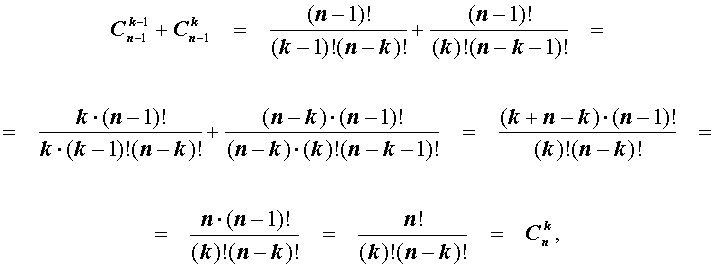
что и требовалось.
Для доказательства равенства 2 положим в формуле бинома Ньютона (1) x = 1, y = 1.
Если же в формуле бинома Ньютона (1) взять x = 1, y = –1, то получится равенство 3.
Перейдем к доказательству равенства 4. С этой целью положим в формуле бинома Ньютона (1) y = 1
|
|
(3) |
Воспользовавшись очевидным равенством
перепишем формулу (3) в другом виде
|
|
(4) |
Если теперь перемножить формулы (3) и (4), то мы получим равенство:
|
|
(5) |
Если к левой части формулы (5) применить формулу бинома Ньютона, а затем, раскрыв в правой части скобки и приведя подобные члены, приравнять коэффициенты при xn в левой и в правой частях, то мы получим следующее равенство:
что и требовалось.