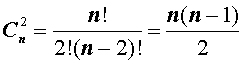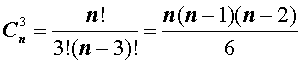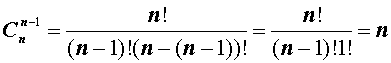Комбинаторика: размещения и сочетания

Оглавление:

Факториалы

Перестановки

Размещения

Сочетания

Размещения

Рассмотрим следующую задачу.

      Задача.   9   карточек пронумерованы числами   1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 .   Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?

      Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.

      На первое место можно положить одну из   9   карточек. Для этого есть   9   способов. В каждом из этих   9   способов на второе место можно положить одну из оставшихся   8   карточек. Таким образом, существует

способа, чтобы положить карточки на первое и второе места. В каждом из этих   72   способов на третье место можно положить одну из оставшихся   7   карточек. Следовательно, существует

способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих   504   способов на четвертое место можно положить одну из оставшихся   6   карточек. Отсюда вытекает, что существует

различных способа, чтобы выложить в ряд   4   карточки из набора, состоящего из   9   пронумерованных карточек. Таким образом, при выкладывании карточек можно получить   3024   различных четырехзначных числа.

      Ответ:   3024.

      При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.

      Определение 1. Рассмотрим множество, содержащее   n   элементов, и все его упорядоченные подмножества, содержащие   k   элементов. Каждое из этих подмножеств называют размещением из   n   элементов по   k   элементов.

      Если обозначить символом  число размещений из   n   элементов по   k   элементов, то будет справедлива формула:

      В соответствии с определением факториала, формулу (1) можно также записать в виде:

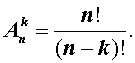
      В задаче множеством из   n   элементов является исходный набор из   9   пронумерованных карточек, а упорядоченным подмножеством из   k   элементов –   4   карточки, выложенные в ряд.

      Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из   9   элементов по   4   элемента, т.е. число 

      В соответствии с формулой (1),

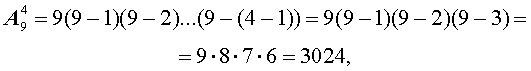
что и было получено в задаче.

      Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.

      Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула

смысл которой заключается в следующем.

      Утверждение. Размещение из   n   элементов по   n   элементов является перестановкой из   n   элементов.

Сочетания

      Определение 2. Рассмотрим множество, состоящее из   n   элементов. Каждое его подмножество, содержащее   k   элементов, называют сочетанием из   n   элементов по   k   элементов.

      Число сочетаний из   n   элементов по   k   элементов обозначается символом 

      Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие   k   элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем   k   элементов (из определения 2), совершить всевозможные перестановки, количество которых равно   k ! ,   то мы получим все размещения.

      Таким образом, справедлива формула:

      Следовательно,

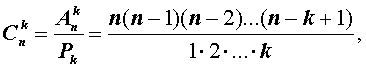
откуда вытекает формула

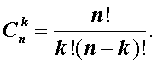(2)

      Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):

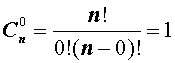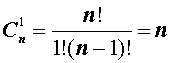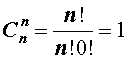      В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):